
ЎѕМвДїЎїОЄБЛЅвДіґОЎ°РЎС§ЙъКй·Ё±ИИьЎ±µДіЙјЁЗйїцЈ¬Лж»ъійИЎБЛ 30 ГыС§ЙъµДіЙјЁЅшРРНіјЖЈ¬ІўЅ«НіјЖЗйїц»жіЙИзНјЛщКѕµДЖµКэ·ЦІјЦ±·ЅНјЈ¬јєЦЄіЙјЁ xЈЁµҐО»Јє·ЦЈ©ѕщВъЧгЎ°50ЎЬxЈј100Ў±Ј®ёщѕЭНјЦРРЕПў»ШґрПВБРОКМвЈє
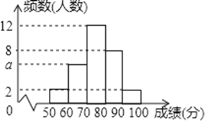
ЈЁ1Ј©НјЦР a µДЦµОЄ Ј»
ЈЁ2Ј©Иф»жЦЖёГСщ±ѕµДЙИРОНіјЖНјЈ¬ФтіЙјЁ x ФЪЎ°80ЎЬxЈј90Ў±Лщ¶ФУ¦ЙИРОµДФІРДЅЗ¶ИКэ ОЄ ¶ИЈ»
ЈЁ3Ј©ґЛґО±ИИь№ІУР 1500 ГыС§ЙъІОјУЈ¬ИфЅ«Ў°xЎЭ80Ў±µДіЙјЁјЗОЄЎ°УЕРгЎ±Ј¬Фт»сµГЎ°УЕРгЎ±µДС§ЙъґуФјУР¶аЙЩИЛЈї
Ўѕґр°ёЎїЈЁ1Ј©6Ј»ЈЁ2Ј©96Ј»ЈЁ3Ј©500
ЎѕЅвОцЎї
ЈЁ1Ј©УГЧЬИЛКэјхИҐЖдЛы·ЦЧйµДИЛКэјґїЙЗуµГaЈ»
ЈЁ2Ј©УГ360ЎгіЛТФіЙјЁФЪ80ЎЬxЈј90µДИЛКэЛщХј±ИАэјґїЙЗуµГґр°ёЈ»
ЈЁ3Ј©УГЧЬИЛКэіЛТФСщ±ѕЦРУЕРгИЛКэЛщХј±ИАэїЙµГЈ®
ЅвЈєЈЁ1Ј©![]() Ј¬
Ј¬
№Кґр°ёОЄЈє6Ј»
ЈЁ2Ј©іЙјЁ x ФЪЎ°80ЎЬxЈј90Ў±Лщ¶ФУ¦ЙИРОµДФІРДЅЗ¶ИКэОЄ![]() Ј¬
Ј¬
№Кґр°ёОЄЈє96Ј»
ЈЁ3Ј©»сµГЎ°УЕРгЎ±µДС§ЙъґуФјУР![]() ЈЁИЛЈ©Ј¬
ЈЁИЛЈ©Ј¬
№Кґр°ёОЄЈє500Ј®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
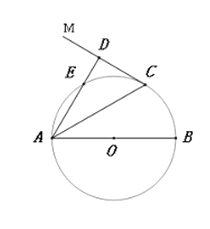
ЎѕМвДїЎїИзНјЈ¬![]() КЗ
КЗ![]() µДЦ±ѕ¶Ј¬µг
µДЦ±ѕ¶Ј¬µг![]() ФЪ
ФЪ![]() ЙПЈ¬№эµг
ЙПЈ¬№эµг![]() Чч
Чч![]() µДЗРПЯ
µДЗРПЯ![]() УЪµг
УЪµг![]() Ѕ»
Ѕ»![]() УЪµг
УЪµг![]() Ј®
Ј®
ЈЁ1Ј©ЗуЦ¤Јє![]() ЖЅ·Ц
ЖЅ·Ц![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() ЗуПЯ¶О
ЗуПЯ¶О![]() µДі¤Ј®
µДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЈ¬ТСЦЄЕЧОпПЯ
ЦРЈ¬ТСЦЄЕЧОпПЯ![]() УлЦ±ПЯ
УлЦ±ПЯ![]() ¶јѕ№э
¶јѕ№э![]() Ўў
Ўў![]() БЅµгЈ¬ёГЕЧОпПЯµД¶ҐµгОЄCЈ®
БЅµгЈ¬ёГЕЧОпПЯµД¶ҐµгОЄCЈ®
ЈЁ1Ј©ЗуґЛЕЧОпПЯєНЦ±ПЯ![]() µДЅвОцКЅЈ»
µДЅвОцКЅЈ»
ЈЁ2Ј©ЙиЦ±ПЯ![]() УлёГЕЧОпПЯµД¶ФіЖЦбЅ»УЪµгEЈ¬ФЪЙдПЯ
УлёГЕЧОпПЯµД¶ФіЖЦбЅ»УЪµгEЈ¬ФЪЙдПЯ![]() ЙПКЗ·сґжФЪТ»µгMЈ¬№эMЧчxЦбµДґ№ПЯЅ»ЕЧОпПЯУЪµгNЈ¬К№µгMЎўNЎўCЎўEКЗЖЅРРЛД±ЯРОµДЛДёц¶ҐµгЈїИфґжФЪЈ¬ЗуµгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ»
ЙПКЗ·сґжФЪТ»µгMЈ¬№эMЧчxЦбµДґ№ПЯЅ»ЕЧОпПЯУЪµгNЈ¬К№µгMЎўNЎўCЎўEКЗЖЅРРЛД±ЯРОµДЛДёц¶ҐµгЈїИфґжФЪЈ¬ЗуµгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ»
ЈЁ3Ј©ЙиµгPКЗЦ±ПЯ![]() ПВ·ЅЕЧОпПЯЙПµДТ»¶ЇµгЈ¬µ±
ПВ·ЅЕЧОпПЯЙПµДТ»¶ЇµгЈ¬µ±![]() Гж»эЧоґуК±Ј¬ЗуµгPµДЧш±кЈ¬ІўЗу
Гж»эЧоґуК±Ј¬ЗуµгPµДЧш±кЈ¬ІўЗу![]() Гж»эµДЧоґуЦµЈ®
Гж»эµДЧоґуЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪБвРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬°ґТФПВІЅЦиЧчНјЈєўЩ·Ц±рТФµг
Ј¬°ґТФПВІЅЦиЧчНјЈєўЩ·Ц±рТФµг![]() єНµг
єНµг![]() ОЄФІРДЈ¬ОЄФІРДЈ¬ґуУЪєЕ
ОЄФІРДЈ¬ОЄФІРДЈ¬ґуУЪєЕ![]() µДі¤ОЄ°лѕ¶ГжєьЈ¬БЅ»ЎЅ»УЪµг
µДі¤ОЄ°лѕ¶ГжєьЈ¬БЅ»ЎЅ»УЪµг![]() Ј¬
Ј¬![]() ЈєўЪЧцЦ±ПЯ
ЈєўЪЧцЦ±ПЯ![]() Ј¬ЗТ
Ј¬ЗТ![]() ЗЎєГѕ№эµг
ЗЎєГѕ№эµг![]() Ј¬Ул
Ј¬Ул![]() Ѕ»УЪµг
Ѕ»УЪµг![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј¬Фт
Ј¬Фт![]() µДЦµОЄЈЁ Ј©
µДЦµОЄЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
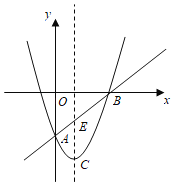
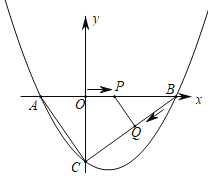
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯУлxЦбЅ»УЪAЎўBБЅµг(µгAФЪµгBЧуІа)Ј¬УлyЦбЅ»УЪµгCЈ¬ЗТµ±xЈЅ©Ѓ1єНxЈЅ3К±Ј¬yЦµПаµИЈ®Ц±ПЯyЈЅ![]() УлЕЧОпПЯУРБЅёцЅ»µгЈ¬ЖдЦРТ»ёцЅ»µгµДєбЧш±кКЗ6Ј¬БнТ»ёцЅ»µгКЗХвМхЕЧОпПЯµД¶ҐµгMЈ®
УлЕЧОпПЯУРБЅёцЅ»µгЈ¬ЖдЦРТ»ёцЅ»µгµДєбЧш±кКЗ6Ј¬БнТ»ёцЅ»µгКЗХвМхЕЧОпПЯµД¶ҐµгMЈ®
(1)ЗуХвМхЕЧОпПЯµД±нґпКЅЈ®
(2)¶ЇµгPґУФµгOіц·ўЈ¬ФЪПЯ¶ОOBЙПТФГїГл1ёцµҐО»і¤¶ИµДЛЩ¶ИПтµгBФЛ¶ЇЈ¬Н¬К±µгQґУµгBіц·ўЈ¬ФЪПЯ¶ОBCЙПТФГїГл2ёцµҐО»і¤¶ИµДЛЩ¶ИПтµгCФЛ¶ЇЈ¬µ±Т»ёцµгµЅґпЦХµгК±Ј¬БнТ»ёцµгБўјґНЈЦ№ФЛ¶ЇЈ¬ЙиФЛ¶ЇК±јдОЄtГлЈ®
ўЩЗуtµДИЎЦµ·¶О§Ј®
ўЪИфК№ЎчBPQОЄЦ±ЅЗИэЅЗРОЈ¬ЗлЗуіц·ыєПМхјюµДtЦµЈ»
ўЫtОЄєОЦµК±Ј¬ЛД±ЯРОACQPµДГж»эУРЧоРЎЦµЈ¬ЧоРЎЦµКЗ¶аЙЩЈїЦ±ЅУРґіцґр°ёЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
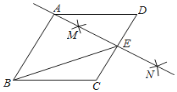
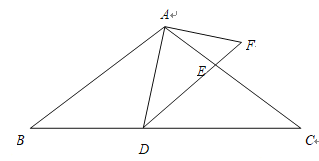
ЎѕМвДїЎїИзНјЈ¬ТСЦЄMКЗЖЅРРЛД±ЯРОABCDЦРAB±ЯµДИэµИ·ЦµгЈ¬BDУлCMЅ»УЪEЈ¬ФтТхУ°Ії·ЦГж»эУлЖЅРРЛД±ЯРОГж»э±ИОЄ_____Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїІДБПТ»ЈєТ»ёцґуУЪ1µДХэХыКэЈ¬Иф±»![]() іэУа1Ј¬±»
іэУа1Ј¬±»![]() іэУа1Ј¬±»
іэУа1Ј¬±»![]() іэУа1ЎЎЈ¬±»3іэУа1Ј¬±»2іэУа1Ј¬ДЗГґіЖХвёцХэХыКэОЄЎ°Гч
іэУа1ЎЎЈ¬±»3іэУа1Ј¬±»2іэУа1Ј¬ДЗГґіЖХвёцХэХыКэОЄЎ°Гч![]() АсЎ±КэЈЁ
АсЎ±КэЈЁ![]() ИЎЧоґуЈ©Ј¬АэИзЈє73ЈЁ±»5іэУа3Ј©±»4іэУа1Ј¬±»3іэУа1Ј¬±»2іэУа1Ј¬ДЗГґ73ОЄЎ°ГчЛДАсЎ±КэЈ®
ИЎЧоґуЈ©Ј¬АэИзЈє73ЈЁ±»5іэУа3Ј©±»4іэУа1Ј¬±»3іэУа1Ј¬±»2іэУа1Ј¬ДЗГґ73ОЄЎ°ГчЛДАсЎ±КэЈ®
ІДБП¶юЈєЙи![]() Ј¬ЎЎЈ¬3Ј¬2µДЧоРЎ№«±¶КэОЄ
Ј¬ЎЎЈ¬3Ј¬2µДЧоРЎ№«±¶КэОЄ![]() Ј¬ДЗГґЎ°Гч
Ј¬ДЗГґЎ°Гч![]() АсЎ±КэїЙТФ±нКѕОЄ
АсЎ±КэїЙТФ±нКѕОЄ![]() ЈЁ
ЈЁ![]() ОЄХэХыКэЈ©Ј¬АэИзЈє6Ј¬5Ј¬4Ј¬3Ј¬2µДЧоРЎ№«±¶КэОЄ60Ј¬ДЗГґЎ°ГчБщАсЎ±КэїЙТФ±нКѕОЄ
ОЄХэХыКэЈ©Ј¬АэИзЈє6Ј¬5Ј¬4Ј¬3Ј¬2µДЧоРЎ№«±¶КэОЄ60Ј¬ДЗГґЎ°ГчБщАсЎ±КэїЙТФ±нКѕОЄ![]() ЈЁ
ЈЁ![]() ОЄХэХыКэЈ©
ОЄХэХыКэЈ©
ЈЁ1Ј©ЗуіцЧоРЎµДИэО»Ў°ГчИэАсЎ±КэЈ»
ЈЁ2Ј©Т»ёцЎ°ГчЛДАсЎ±КэУлЎ°ГчОеАсЎ±КэµДєНОЄ170Ј¬ЗуіцХвБЅёцКэЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬µг
Ј¬µг![]() ОЄ
ОЄ![]() ±ЯЙПµДТ»ёц¶ЇµгЈЁµг
±ЯЙПµДТ»ёц¶ЇµгЈЁµг![]() І»Улµг
І»Улµг![]() Ўўµг
Ўўµг![]() ЦШєПЈ©Ј®ТФ
ЦШєПЈ©Ј®ТФ![]() ОЄ¶ҐµгЧч
ОЄ¶ҐµгЧч![]() Ј¬ЙдПЯ
Ј¬ЙдПЯ![]() Ѕ»
Ѕ»![]() ±ЯУЪµг
±ЯУЪµг![]() Ј¬№эµг
Ј¬№эµг![]() Чч
Чч![]() Ѕ»ЙдПЯ
Ѕ»ЙдПЯ![]() УЪµг
УЪµг![]() .
.
ЈЁ1Ј©ЗуЦ¤Јє![]() Ј»
Ј»
ЈЁ2Ј©µ±![]() ЖЅ·Ц
ЖЅ·Ц![]() К±Ј¬Зу
К±Ј¬Зу![]() µДі¤Ј»
µДі¤Ј»
ЈЁ3Ј©µ±![]() КЗµИСьИэЅЗРОК±Ј¬Зу
КЗµИСьИэЅЗРОК±Ј¬Зу![]() µДі¤Ј®
µДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
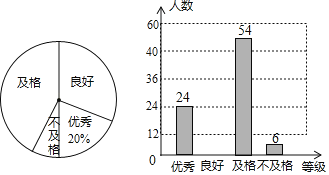
ЎѕМвДїЎї2019ДкИ«№ъЗаЙЩДкЅы¶ѕЦЄК¶ѕєИьїЄКјТФАґЈ¬ДіКРЗаЙЩДкС§ЙъУ»ФѕІОјУЈ¬ПЖЖрБЛС§П°Ѕы¶ѕЦЄК¶µДИИі±Ј¬Ѕы¶ѕЦЄК¶ѕєИьµДіЙјЁ·ЦОЄЛДёцµИј¶ЈєУЕРгЈ¬БјєГЈ¬ј°ёсЈ¬І»ј°ёсЈ®ОЄБЛБЛЅвёГКР№гґуС§ЙъІОјУЅы¶ѕЦЄК¶ѕєИьµДіЙјЁЈ¬ійИЎБЛІї·ЦС§ЙъµДіЙјЁЈ¬ёщѕЭійІйЅб№ыЈ¬»жЦЖБЛИзПВБЅ·щІ»НкХыµДНіјЖНјЈє
ЈЁ1Ј©±ѕґОійІйµДИЛКэКЗЎЎ ЎЎЈ»ЙИРОНіјЖНјЦРІ»ј°ёсС§ЙъЛщХјµДФІРДЅЗµД¶ИКэОЄЎЎ ЎЎЈ»
ЈЁ2Ј©І№И«МхРОНіјЖНјЈ»
ЈЁ3Ј©ИфДіРЈУР2000ГыС§ЙъЈ¬ЗлДгёщѕЭµчІйЅб№ы№АјЖёГРЈС§ЙъЦЄК¶ѕєИьіЙјЁОЄЎ°УЕРгЎ±єНЎ°БјєГЎ±БЅёцµИј¶№ІУР¶аЙЩИЛЈї
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com