
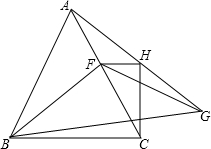
 已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.
已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.
| ||
| 2 |
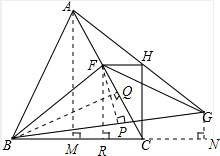 解:作AM⊥BC,BQ⊥AC,FP⊥BQ,FR⊥BC,GN⊥BC延长线于N,
解:作AM⊥BC,BQ⊥AC,FP⊥BQ,FR⊥BC,GN⊥BC延长线于N,
| ||
| 2 |
| 3 |
| BQ |
| BN |
| BF |
| BG |
| QF |
| GN |
| ||||
| BN |
| b | ||
|
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BF2-BQ2 |
b2-
|
| 1 |
| 2 |
| 4b2-3a2 |
| QF•BG |
| BF |
| ||||||
| b |
| ||
| 2 |
| 4b2-3a2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 4b2-3a2 |
| ||
| 4 |
| 4b2-3a2 |
| 1 |
| 2 |
| 1 |
| 2 |
| b2-3a2 |
| ||
| 2 |
| ||
| 4 |
| 4b2-3a2 |


 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com