
分析 由题意可得,原式可化为$\frac{1}{2}$+($\frac{1}{3}+\frac{2}{3}$)+($\frac{1}{4}+\frac{2}{4}+\frac{3}{4}$)+…+($\frac{1}{100}+\frac{2}{100}+…+\frac{98}{100}+\frac{99}{100}$),然后展开,观察其规律,即可解答本题.
解答 解:($\frac{1}{2}$+$\frac{1}{3}+\frac{1}{4}+$…+$\frac{1}{99}+\frac{1}{100}$)+($\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+$…+$\frac{2}{99}+\frac{2}{100}$)+…+($\frac{98}{99}+\frac{98}{100}$)+$\frac{99}{100}$
=$\frac{1}{2}$+($\frac{1}{3}+\frac{2}{3}$)+($\frac{1}{4}+\frac{2}{4}+\frac{3}{4}$)+…+($\frac{1}{100}+\frac{2}{100}+…+\frac{98}{100}+\frac{99}{100}$)
=$\frac{1}{2}+1+(1+\frac{1}{2})$+2+(2+$\frac{1}{2}$)+3+(3+$\frac{1}{2}$)+…+(49+$\frac{1}{2}$)
=$\frac{1}{2}×50+(1+2+3+…+49)×2$
=25+$\frac{49×(1+49)}{2}×2$
=25+2450
=2475.
点评 本题考查有理数的混合运算,解题的关键的是先对式子展开能够观察出其中的规律.


科目:初中数学 来源: 题型:解答题
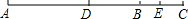 如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E为BC的中点.
如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
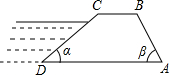 如图,拦水坝的横断面为四边形ABCD,且AD∥BC,上面CB=5m,迎水面的坡度为1:$\sqrt{3}$,背水面坡度为1:1,坝高为4m,求:
如图,拦水坝的横断面为四边形ABCD,且AD∥BC,上面CB=5m,迎水面的坡度为1:$\sqrt{3}$,背水面坡度为1:1,坝高为4m,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
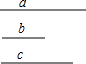 如图,已知线段a,b,c(a>c>b),画两条线段,使它分别等于a+$\frac{1}{2}b$-c•$\frac{1}{2}$(2a+b-c).
如图,已知线段a,b,c(a>c>b),画两条线段,使它分别等于a+$\frac{1}{2}b$-c•$\frac{1}{2}$(2a+b-c).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com