
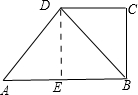
 解:如图,过点D作DE⊥AB于点E;
解:如图,过点D作DE⊥AB于点E;| 133 |
| 133 |
| 36 | ||
|
| 1 |
| 2 |
| 133 |
| 133 |
| 36 | ||
|
906
| ||
| 133 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
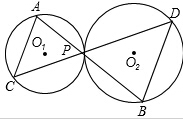 如图,已知⊙O1和⊙O2外切于点P,过点P.作直线AB、CD,AB分别交⊙O1和⊙O2于点A、B,CD分别交⊙O1和⊙O2于C、D两点,求证:AC∥BD.
如图,已知⊙O1和⊙O2外切于点P,过点P.作直线AB、CD,AB分别交⊙O1和⊙O2于点A、B,CD分别交⊙O1和⊙O2于C、D两点,求证:AC∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:
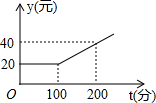 已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示.
已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示.| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:
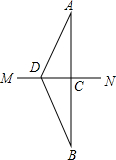 如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?
如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
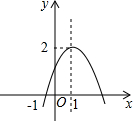 如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:
如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com