
分析 (1)根据同底数幂的乘法运算性质计算即可;
(2)先算乘方,再算乘法即可;
(3)先根据负整数指数幂、零整数指数幂的意义分别化简,再进行加减运算即可;
(4)先算乘方,再算乘除即可;
(5)先将(p-q)4与(p-q)2 分别转化为(q-p)4与(q-p)2,再根据同底数幂的除法运算性质计算即可;
(6)逆用同底数幂的乘法与积的乘方运算性质计算即可.
解答 解:(1)x3•x•x2=x6;
(2)(-a3)2•(-a2)3
=a6•(-a6)
=-a12;
(3)($\frac{2}{3}$)-1+(π-3)0-(-2)-2
=$\frac{3}{2}$+1-$\frac{1}{4}$
=$\frac{9}{4}$;
(4)(b2n)3(b3)4n÷(b5)n
=b6n•b12n÷b5n
=b13n;
(5))(p-q)4÷(q-p)3•(p-q)2
=(q-p)4÷(q-p)3•(q-p)2
=(q-p)3;
(6)${({1\frac{2}{3}})^{2006}}×{({{-}0.6})^{2007}}$
=($\frac{5}{3}$)2006×(-$\frac{3}{5}$)2006×(-$\frac{3}{5}$)
=[$\frac{5}{3}$×(-$\frac{3}{5}$)]2006×(-$\frac{3}{5}$)
=$-\frac{3}{5}$.
点评 本题考查了整式的混合运算,熟练掌握幂的运算性质是解题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
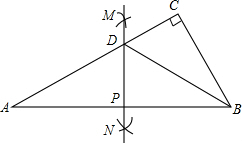 如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )
如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )| A. | 直线AB是线段MN的垂直平分线 | B. | CD=$\frac{1}{2}$AD | ||
| C. | BD平分∠ABC | D. | S△APD=S△BCD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 1.2 | 1.3 | 1.4 | 1.5 |
| x2+x-3 | -0.36 | -0.01 | 0.36 | 0.75 |
| A. | 1.3 | B. | 1.2 | C. | 1.5 | D. | 1.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com