
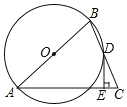
【题目】如图,在![]() 中,
中,![]() ,点D在BC上,
,点D在BC上,![]() ,过点D作
,过点D作![]() ,垂足为E,
,垂足为E,![]() 经过A,B,D三点.
经过A,B,D三点.
![]() 求证:AB是
求证:AB是![]() 的直径;
的直径;
![]() 判断DE与
判断DE与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
![]() 若
若![]() 的半径为10m,
的半径为10m,![]() ,求DE的长.
,求DE的长.
【答案】(1)证明见解析;(2)![]() 与圆O相切,理由见解析;(3)
与圆O相切,理由见解析;(3)![]() .
.
【解析】
(1)连接AD,由AB=AC,BD=CD,利用等腰三角形三线合一性质得到AD⊥BC,利用90°的圆周角所对的弦为直径即可得证;
(2)DE与圆O相切,理由为:连接OD,由O、D分别为AB、CB中点,利用中位线定理得到OD与AC平行,利用两直线平行内错角相等得到∠ODE为直角,再由OD为半径,即可得证;
(3)由AB=AC,且∠BAC=60°,得到三角形ABC为等边三角形,设AC与![]() 交于点F,连接BF,DE为△CBF中位线,求出BF的长,即可确定出DE的长.
交于点F,连接BF,DE为△CBF中位线,求出BF的长,即可确定出DE的长.
![]() 证明:如图
证明:如图
连接AD,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 为圆O的直径;
为圆O的直径;
![]() 与圆O相切,理由为:
与圆O相切,理由为:
证明:连接OD,
![]() 、D分别为AB、BC的中点,
、D分别为AB、BC的中点,
![]() 为
为![]() 的中位线,
的中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为圆的半径,
为圆的半径,
![]() 与圆O相切;
与圆O相切;
![]() 解:
解:![]() ,
,![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
设AC与![]() 交于点F,连接BF,
交于点F,连接BF,
![]() 为圆O的直径,
为圆O的直径,
![]() ,
,
![]() ,
,![]() ,
,
![]() 为BC中点,
为BC中点,
![]() 为CF中点,即DE为
为CF中点,即DE为![]() 中位线,
中位线,
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
则![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
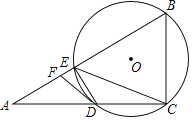
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
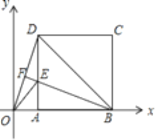
【题目】如图,在平面直角坐标系中,边长为![]() 的正方形ABCD的顶点A,B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E,连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,则点M的坐标_____.
的正方形ABCD的顶点A,B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E,连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,则点M的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
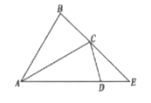
【题目】如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
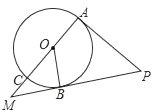
【题目】如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当MB=4,MC=2时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价不低于100元,但不超过180元.设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获利为
(万件),年获利为![]() (万元),该产品年销售量
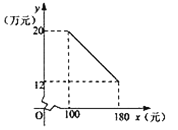
(万元),该产品年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数表达式,并写出
之间的函数表达式,并写出![]() 的取值范围;
的取值范围;
(2)求第一年的年获利![]() 与
与![]() 之间的函数表达式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
之间的函数表达式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
(3)在(2)的条件下.即在盈利最大或亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利不低于1370万元?若能,求出第二年的售价在什么范围内;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明在网上经营一家水果店,销售的草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒。为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元。每笔订单顾客网上支付成功后,李明会得到支付款的80%。在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA、GB、GC、GD、EF,若∠AGD=∠BGC.
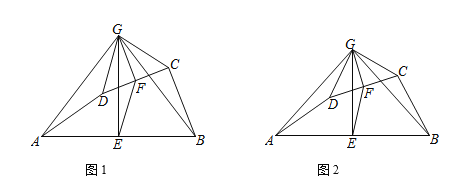
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com