
分析 首先根据有理数乘方的运算方法,分别求出(-1)2003,(-1)2004,-22,(-3)2的值各是多少;然后根据有理数大小比较的方法,判断出这四个数中,最大的数、最小的数各是多少即可.
解答 解:(-1)2003=-1,(-1)2004=1,-22=-4,(-3)2=9,
∵9>1>-1>-4,
∴(-3)2>(-1)2004>(-1)2003>-22,
∴在(-1)2003,(-1)2004,-22,(-3)2这四个数中,最大的数是(-3)2,最小的数是-22.
故答案为:(-3)2;-22.
点评 (1)此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
(2)此题还考查了有理数的乘方的运算方法,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠ABC=60°,对角线AC、BD交于点O,以点B为圆心,BC为半径作圆与BD交于点E,则图中阴影部分的面积为$\frac{4π}{3}$-2$\sqrt{3}$.
如图,在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠ABC=60°,对角线AC、BD交于点O,以点B为圆心,BC为半径作圆与BD交于点E,则图中阴影部分的面积为$\frac{4π}{3}$-2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $|{\vec a}|$$\vec e$=$\vec a$ | B. | $\vec a$$|{\vec e}|$=$\vec a$ | C. | $\frac{1}{\vec a}$$\vec a$=$\vec e$ | D. | $\frac{{|{\vec a}|}}{{|{\vec e}|}}$=$\vec a$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图2,已知△ABC中,∠ACB=90°,AC=b,BC=a.将△ABC绕点C按顺时针方向旋转90°,点B旋转到点B′,点A旋转到点A′.
如图2,已知△ABC中,∠ACB=90°,AC=b,BC=a.将△ABC绕点C按顺时针方向旋转90°,点B旋转到点B′,点A旋转到点A′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
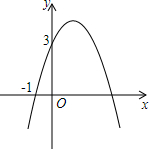 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
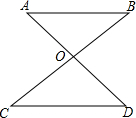 如图,AD、BC相交于点O,AO=OD,只要添加以下条件中的一个条件,就能证明△ABO≌△DCO,则这样的条件有①②④⑤.
如图,AD、BC相交于点O,AO=OD,只要添加以下条件中的一个条件,就能证明△ABO≌△DCO,则这样的条件有①②④⑤.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com