
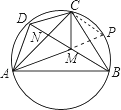
【题目】如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN.
求证:(1)M为BD的中点;(2)![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)要证M为BD的中点,即证BM=DM,由∠BAM=∠DAN,∠BCM=∠DCN,及圆周角的性质易证明△BAM∽△CBM,△DAM∽△CDM得出比例的乘积形式,可证明BM=DM;
(2)欲证![]() ,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.
,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.
试题解析:(1)根据同弧所对的圆周角相等,得∠DAN=∠DBC,∠DCN=∠DBA,
又∵∠DAN=∠BAM,∠BCM=∠DCN,
∴∠BAM=∠MBC,∠ABM=∠BCM,
∴△BAM∽△CBM,
∴![]() ,即BM2=AMCM ,①
,即BM2=AMCM ,①
又∠DCM=∠DCN+∠NCM=∠BCM+∠NCM=∠ACB=∠ADB,
∠DAM=∠MAC+∠DAN=∠MAC+∠BAM=∠BAC=∠CDM,
∴△DAM∽△CDM,
则![]() ,即DM2=AMCM ,②
,即DM2=AMCM ,②
由式①、②得:BM=DM,
即M为BD的中点;
(2)如图,延长AM交圆于点P,连接CP,
∴∠BCP=∠PAB=∠DAC=∠DBC,
∵PC∥BD,
∴![]() , ③
, ③
又∵∠MCB=∠DCA=∠ABD,∠DBC=∠PCB,
∴∠ABC=∠MCP,
而∠ABC=∠APC,
则∠APC=∠MCP,
有MP=CM,④
由式③、④得: ![]() .
.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论.
(3)若∠B=30°,计算S△DAC:S△ABC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,BC=10,tan∠ABC=![]() ,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
(1)当AE∥BC(如图(1))时,求⊙O的半径;
(2)设BO=x,AE=y,求y关于x的函数关系式;
(3)若以A为圆心的⊙A与⊙O有公共点D、E,当恰好也过点C时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
云阳县多集合生态农业有限公司在2018年种植玉米的平均亩产量为0. 75吨,该公司总结了种植玉米的经验,2019年该公司种植玉米的情况是:种植面积比2018年减少了10%、平均亩产量比2018年增加了0. 2吨,总产量比2018年增加了8. 4吨.
(1)求2018年该公司种植玉米的面积;
(2)若2019年该公司种植玉米的人数比2018年少了12人,人均种植面积比2018年增加了17%,求2019年该公司种植玉米的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.
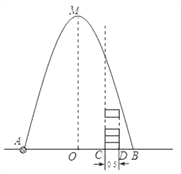
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元。
(1)求文具袋和圆规的单价。
(2)学校准备购买文具袋20个,圆规若干,文具店给出两种优惠方案:
方案一:购买一个文具袋还送1个圆规。
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.
①设购买面规m个,则选择方案一的总费用为______,选择方案二的总费用为______.
②若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A.点B同时出发,沿三角形的边运动,已知点M的速度为2cm/s,点N的速度为3cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动 秒后,△AMN是等边三角形?
(2)点M、N在BC边上运动时,运动 秒后得到以MN为底边的等腰三角形△AMN?
(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com