
【题目】如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为_____.

【答案】![]()
【解析】
分别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,先根据全等三角形的判定定理得出△BCE≌△ACF,故可得出CF及CE的长,在Rt△ACF中根据勾股定理求出AC的长,再由相似三角形的判定得出△CDG∽△CAF,故可得出CD的长,在Rt△BCD中根据勾股定理即可求出BD的长.
解:别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,
∵△ABC是等腰直角三角形,
∴AC=BC,
∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,
∴∠EBC=∠ACF,∠BCE=∠CAF,
在△BCE与△ACF中,
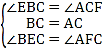
∴△BCE≌△ACF(ASA)
∴CF=BE,CE=AF,
∵l1与l2的距离为1,l2与l3的距离为3,
∴CF=BE=3,CE=AF=3+1=4,
在Rt△ACF中,
∵AF=4,CF=3,
∴AC=5,
∵AF⊥l3,DG⊥l3,
∴△CDG∽△CAF,
![]() ,
,
![]() ,
,
![]() ,
,
在Rt△BCD中,
∵![]() ,BC=5,
,BC=5,
所以![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
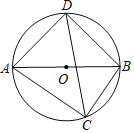
【题目】如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 分别在两个半圆上(不与点
分别在两个半圆上(不与点![]() 重合),
重合),![]() 的长分别是关于
的长分别是关于![]() 的方程
的方程![]()
![]() 的两个实数根.
的两个实数根.
(1)![]() 的值为_____;
的值为_____;
(2)连接![]() 三者之间的等量关系为_____.
三者之间的等量关系为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.

(1)当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.
(2)如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:
①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.
(参考数据:![]() ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高农田利用效益,某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾稻”轮作模式.某农户有农田20亩,去年开始实施“虾稻”轮作,去年出售小龙虾每千克获得的利润为32元(利润=售价﹣成本).由于开发成本下降和市场供求关系变化,今年每千克小龙虾的养殖成本下降25%,售价下降10%,出售小龙虾每千克获得利润为30元.
(1)求去年每千克小龙虾的养殖成本与售价;
(2)该农户今年每亩农田收获小龙虾100千克,若今年的水稻种植成本为600元/亩,稻谷售价为25元/千克,该农户估计今年可获得“虾稻”轮作收入不少于8万元,则稻谷的亩产量至少会达到多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为创建《国家义务教育优质均衡发展区》,自2016年以来加大了教育经费的投入,2016年该区投入教育经费9000万元,2018年投入教育经费12960万元,假设该区这两年投入教育经费的年平均增长率相同
(1)求这两年该区投入教育经费的年平均增长率
(2)若该区教育经费的投入还将保持相同的年平均增长率,请你预算2019年该区投入教育经费多少万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组有规律的图案,它们是由边长相同的小正方形组成的,其中部分小正方形涂有阴影,依此规律,第2018个图案中涂有阴影的小正方形个数为( )

A.8073B.8072C.8071D.8070
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y1,y2分别是关于x的函数,如果函数y1和y2的图象有交点,那么称y1,y2为“亲密函数”,交点称为函数y1和y2的“亲密点”;若两函数图象有两个交点,横坐标分别是x1,x2,称L=|x1﹣x2|为函数y1和y2的“亲密度”,特别地,若两函数图象只有一个交点,则两函数的“亲密度”L=0.
(1)已知一次函数y1=2x﹣5与反比例函数y2=![]() ,请判断函数y1和y2是否为“亲密函数”,若是,请写出“亲密点”及“亲密度”L,若不是,请说明理由;
,请判断函数y1和y2是否为“亲密函数”,若是,请写出“亲密点”及“亲密度”L,若不是,请说明理由;
(2)已知二次函数y=ax2﹣6x+c与x轴只有一个交点,与一次函数y=x﹣1的“亲密度”L=3,求二次数的解析式;
(3)已知“亲密函数”y1=ax﹣2和y2=![]() 的“亲密度”L=0,“亲密点”为P(x0,y0),将过P的抛物线y=ax2+bx+c(b>0)进行平移,点P的对应点为P1(1﹣m,2b﹣1),平移后的抛物线仍经过点P,当m≥﹣
的“亲密度”L=0,“亲密点”为P(x0,y0),将过P的抛物线y=ax2+bx+c(b>0)进行平移,点P的对应点为P1(1﹣m,2b﹣1),平移后的抛物线仍经过点P,当m≥﹣![]() 时,求平移后抛物线的顶点所能达到的最高点的坐标.
时,求平移后抛物线的顶点所能达到的最高点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com