
【题目】如图,在平面直角坐标系中,矩形AOBC的边长为AO=6,AC=8,
(1)如图①,E是OB的中点,将△AOE沿AE折叠后得到△AFE,点F在矩形AOBC内部,延长AF交BC于点G.求点G的坐标;
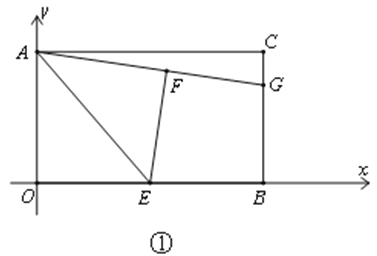
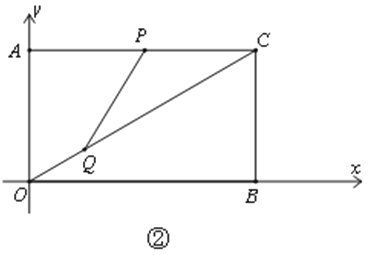
(2)定义:若以不在同一直线上的三点中的一点为圆心的圆恰好过另外两个点,这样的圆叫做黄金圆.如图②,动点P以每秒2个单位的速度由点C向点A沿线段CA运动,同时点Q以每秒4个单位的速度由点O向点C沿线段OC运动;求:当 PQC三点恰好构成黄金圆时点P的坐标.
【答案】(1)(8,![]() );(2)
);(2)![]() ,
,![]() ,
,![]() .
.
【解析】
试题(1)由折叠对称的性质可得DAOE≌DAFE,从而推出DEFG≌DEBG,得到DAOE∽DAEG,因此AE2=AO×AG,在Rt△AOE中,由勾股定理可得AE2=36+16=52,从而得AG=![]() ,在Rt△ABM中,由勾股定理可得CG=
,在Rt△ABM中,由勾股定理可得CG=![]() ,从而BG=
,从而BG=![]() ,得到G的坐标为(8,
,得到G的坐标为(8,![]() );(2)分点C为黄金圆的圆心,点P为黄金圆的圆心,点Q为黄金圆的圆心三种情况讨论即可.
);(2)分点C为黄金圆的圆心,点P为黄金圆的圆心,点Q为黄金圆的圆心三种情况讨论即可.
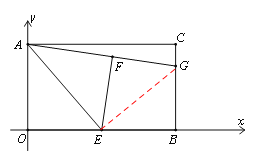
试题解析:(1)如图,连接EG,
由题意得:DAOE≌DAFE,∴EFG=OBC=900.
又∵E是OB的中点,∴EG=EG,EF=EB=4.∴DEFG≌DEBG.
∴FEG=BEG,AOB=AEG=900. ∴DAOE∽DAEG,AE2=AO×AG.
又在Rt△AOE中,∵AO=6,OE=4,∴AE2=36+16=52.
∴52=6×AG,AG=![]() .
.
在Rt△ABM中,由勾股定理可得CG=![]() ,∴BG=
,∴BG=![]() .
.
∴G的坐标为(8,![]() ) .
) .
(2)设运动的时间为t秒,
当点C为黄金圆的圆心时,则CQ=CP,
即:2t=10—4t,得到t=![]() ,此时CP=
,此时CP=![]() ,AP=
,AP=![]() ,P点坐标为
,P点坐标为![]() .
.
当点P为黄金圆的圆心时,则PC=PQ,
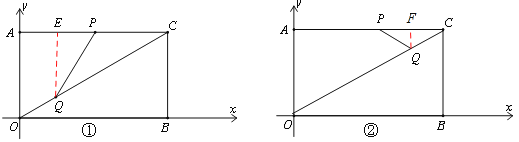
如图①,过点Q作AC的垂线交AC于点E,CQ=10—4t,CP=2t.
由三角形相似可知:EQ=![]() CQ=
CQ=![]() ,PE=
,PE=![]() ,
,
则![]() ,
,![]() 化简得:
化简得:![]() ,
,
解得![]() (舍去).
(舍去).
此时,AP=![]() ,P点坐标为
,P点坐标为![]() .
.
当点Q为黄金圆的圆心时,则QC=PQ,
如图②,过点Q作AC的垂线交AC于点F,CQ=10—4t,CP=2t.
由三角形相似可知:QF=![]() ,PF=
,PF=![]() ,
,
则![]() ,整理得
,整理得![]() .
.
解得![]() (舍去).
(舍去).
此时,AP=![]() ,P点坐标为
,P点坐标为![]() .
.
综上所述,P点坐标为![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】师徒二人各加工同样多的零件,师父每小时加工200个,徒弟每小时加工125个.若徒弟先加工段时间之后,师父才开始工作师父工作2小时后发现自己加工的零件个数和徒弟加工的个数刚好相同,如图是师徒两人完成的零件个数之差y(个)与徒弟工作的时间x(小时)之间的函数图象,根据图象回答问题:
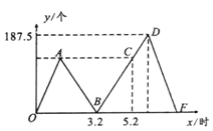
(1)求出点A的坐标,并解释该点坐标表示的实际意义;
(2)求出线段BD的函数表达式;
(3)求徒弟这次加工的零件总数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们知道,分式类比分数,分数中有真分数、假分数、带分数、类似的,在分式中,也规定真分式、假分式、带分式;在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式.例如,分式![]() ,
,![]() 是假分式,一个假分式可以化为带分式,即化为一个整式与一个真分式的和,例如,
是假分式,一个假分式可以化为带分式,即化为一个整式与一个真分式的和,例如,![]() .(注意带分式中整式与真分式之间的符号不能省略)
.(注意带分式中整式与真分式之间的符号不能省略)
请根据以上方法,解决下列问题;
(1)请根据以上信息,任写一个真分式 .
(2)已知:![]() ;
;
①当![]() 时,若
时,若![]() 与
与![]() 都为正整数,求
都为正整数,求![]() 的值;
的值;
②计算![]() ,设
,设![]() ,探索
,探索![]() 是否有最小值,若有,请求出
是否有最小值,若有,请求出![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 分别是
分别是![]() 的边
的边![]() 、
、![]() 的中点,边
的中点,边![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,现在下列四个结论:
,现在下列四个结论:
①![]() ,②
,②![]() 平分
平分![]() ,③
,③![]() ,④
,④![]() .
.
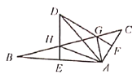
则其中正确的结论有( ).
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王明同学随机抽查某市![]() 个小区所得到的绿化率情况,结果如下表:
个小区所得到的绿化率情况,结果如下表:
小区绿化率 |
|
|
|
|
小区个数 |
|
|
|
|
则关于这![]() 个小区的绿化率情况,下列说法错误的是( )
个小区的绿化率情况,下列说法错误的是( )
A. 极差是13% B. 众数是25% C. 中位数是25% D. 平均数是26.2%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com