练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
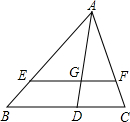
    如图，在△ABC中，AD是高，点E在AB上，EF∥BC，分别交AC、AD于点F、G，且
    BC
    EF
    =
    5
    3
    ．求：
    （1）
    AD
    AG
    的值；
    （2）△AEF与△ABC的面积比．
    考点：相似三角形的判定与性质
    专题：
    分析：（1）易证△AEF∽△ABC，
    AF
    AC
    =
    AG
    AD
    ，即可求得
    AG
    AD
    =
    EF
    BC
    ，即可解题；
    （2）根据相似三角形面积的比值等于相似比的平方即可解题．
    解答：解：（1）∵EF∥BC，
    ∴△AEF∽△ABC，
    AF
    AC
    =
    AG
    AD
    ，
    ∴
    AF
    AC
    =
    EF
    BC
    ，
    ∴
    AG
    AD
    =
    EF
    BC
    ，
    ∴
    AD
    AG
    =
    BC
    EF
    =
    5
    3
    ；
    （2）∵△AEF∽△ABC，
    ∴△AEF与△ABC的面积比=(
    EF
    BC
    )    2    =
    9
    25
    ．
    点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，考查了相似三角形面积比等于相似比平方得性质，本题中求证△AEF∽△ABC是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是60件，而销售单价每涨1元，就会少售出2件玩具．
    （1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
    销售单价（元）x
    销售量y（件）
     
    销售玩具获得利润w（元）
     
    （2）在（1）问条件下，若商场获得了792元销售利润，求该玩具销售单价x应定为多少元．
    （3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于48件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一群小孩子分栗子，如果每人6颗，则剩2颗，如果每人7颗，缺2颗，一共有多少小孩子？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在数学的学习过程中，我们经常用一下的探索过程解决相关问题数学问题：平面内有1个点，如果在平面内再添加n个点，并过这n+1个点中任意两点画直线，那么最多可以画出多少条直线？
    添加点的个数图形最多可画出的直线条数
    11
    2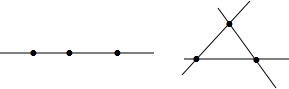3
    3？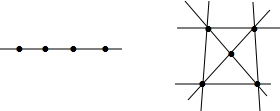
    ………

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    两地相距n km，提速前火车从一地到另一地要用t h，提速后行车时间减少了0.5h，提速后火车的速度比原来速度快了多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

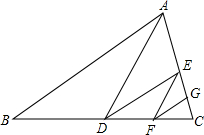    如图，AD是△ABC的中线，DE是△ADC的中线，EF是△DEC的中线，FG是△EFC的中线．
    问题1：△ABD与△ADC的面积有何关系？请说明理由？
    问题2：若△GFC的面积S△GFC=1cm2，则△ABC的面积S△ABC=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，抛物y=x2+bx+c与x轴交于点（1，0）、（2，0），x1、x2是关于x的方程x2+bx+c=0的两个根，则x1+x2=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

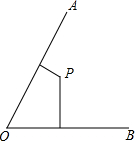    已知∠AOB=60°，P为角内部一点，P到OA、OB的距离分别为1和5，在射线OA上找一点M，在射线OB上找一点N，使PM+PN最小，则最小值为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    沿一张矩形纸较长两边的中点对折后，再对折一次，使两次的折痕平行．如果这两次对折后得到的矩形与原来的矩形纸相似，那么原来矩形纸的长与宽的比为
     
    ．

    查看答案和解析>>

    同步练习册答案