
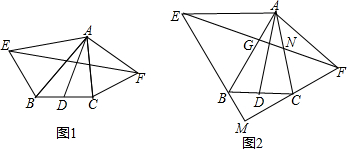
分析 (1)延长AD至H,使DH=AD,连接BH,证明△BDH≌△CDA,得到AC∥BH,得到∠ABH+∠BAC=180°,证明∠ABH=∠EAF即可得到答案;
(2)作AK⊥BC于K,连接CG,根据三角形全等的判定和性质求出AN和CF的长即可.
解答 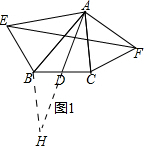 (1)证明:延长AD至H,使DH=AD,连接BH,
(1)证明:延长AD至H,使DH=AD,连接BH,
∵EF=2AD,
∴AH=EF,
在△BDH和△CDA中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDH=∠CDA}\\{DH=AD}\end{array}\right.$,
∴△BDH≌△CDA,
∴HB=AC,∠BHD=∠CAD,
∴AC∥BH,
∴∠ABH+∠BAC=180°,
在△ABH和△EAF中,
$\left\{\begin{array}{l}{AE=AB}\\{HB=AF}\\{AH=EF}\end{array}\right.$,
∴△ABH≌△EAF,
∴∠ABH=∠EAF,
∴∠EAF+∠BAC=180°;
(2)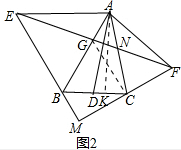 $\frac{AN}{FC}$=$\frac{\sqrt{21}}{7}$,
$\frac{AN}{FC}$=$\frac{\sqrt{21}}{7}$,
证明:作AK⊥BC于K,连接CG,
∵△ABH≌△EAF,
∴∠AEG=∠BAD,
由(1)得,AD=$\frac{1}{2}$EF,又点G为EF中点,
∴EG=AD,
在△EAG和△ABD中,
$\left\{\begin{array}{l}{AE=AB}\\{∠AEG=∠BAD}\\{EG=AD}\end{array}\right.$,
∴△EAG≌△ABD,
∴∠EAG=∠ABC=60°,
∴△AEB是等边三角形,
∴∠ABE=60°,
∴∠CBM=60°,
在△ACD和△FAG中,
$\left\{\begin{array}{l}{AD=FG}\\{AG=CD}\\{AF=AC}\end{array}\right.$,
∴△ACD≌△FAG,
∴∠ACD=∠FAG,∠DAC=∠F,∠ADC=∠FGA,
∵AC=AF,∴∠ACF=∠AFC,
在四边形ABCF中,∠ABC+∠BCF+∠CFA+∠BAF=360°,
则∠BCF=150°,
∴∠BCM=30°,
∴∠BMC=90°,
则BC=2BM,
设BD=a,则CD=BM=AG=a,CM=$\sqrt{3}$a,BG=2BM=2a,则AB=3a,
∵∠ABC=60°,∠AKB=90°,
∴∠BAK=30°,
∴BK=$\frac{3}{2}$a,AK=$\frac{\sqrt{3}a}{2}$,CK=DK=$\frac{1}{2}$a,
则AC=$\sqrt{A{K}^{2}+C{K}^{2}}$=$\sqrt{7}$a,
∵CK=DK,
∴∠ADC=∠ACD,
∵∠ADC=∠FGA,
∴∠AGN=∠ACB,
又∵∠GAN=∠CAB,
∴△GAN∽△CAB,
∴$\frac{AG}{AC}$=$\frac{AN}{AB}$,
∴$\frac{a}{\sqrt{7}a}$=$\frac{AN}{3a}$,
∴AN=$\frac{3\sqrt{7}a}{7}$,
∵FC=CM=$\sqrt{3}$a,
∴$\frac{AN}{FC}$=$\frac{\sqrt{21}}{7}$.
点评 本题考查的是三角形相似的判定和性质、三角形全等的判定和性质,掌握它们的判定定理和性质定理以及直角三角形的性质是解题的关键,注意本题难度较大,解答时要灵活运用所学的知识.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
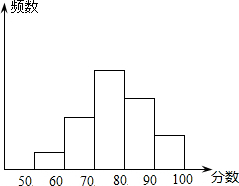 某班同学参加环保知识竞赛,将学生的成绩(得分取整数)进行整理后分成五组,绘制成频数分布直方图如图,图中从左到右各组的小长方形的高的比为1:3:6:4:2,最后一组的频数为6,结合频数分布直方图提供的信息,回答下列问题:
某班同学参加环保知识竞赛,将学生的成绩(得分取整数)进行整理后分成五组,绘制成频数分布直方图如图,图中从左到右各组的小长方形的高的比为1:3:6:4:2,最后一组的频数为6,结合频数分布直方图提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com