练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．我国古代数学家赵爽的《勾股方圆图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图），如果大正方形的面积是16，小正方形的面积是3，直角三角形较短的直角边为a，较长的直角边为b那么（a+b）2的值为（　　）
    A．16B．29C．19D．48

    分析 易求得ab的值，和a2+b2的值，根据完全平方公式即可求得（a+b）2的值，即可解题．

    解答 解：∵大正方形的面积是16，小正方形的面积是3，
    ∴四个直角三角形面积和为16-3=13，即4×$\frac{1}{2}$ab=13，
    ∴2ab=13，a2+b2=16，
    ∴（a+b）2=a2+b2+2ab=16+13=29．
    答：（a+b）2的值为29，
    故选B．

    点评 本题考查了完全平方公式的应用，考查了直角三角形中勾股定理的运用，本题中求得ab的值是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．如图，某小区规划在一个长20米、宽10米的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草．要使每一块花草的面积都为27平方米，那么通道的宽应设计成多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．已知点A（4，y1），B（$\sqrt{2}$，y2），C（-2，y3）都在二次函数y=-2x2的图象上，则y1，y2，y3的大小关系是（　　）
    A．y1＞y2＞y3B．y2＞y3＞y1C．y3＞y2＞y1D．y2＞y1＞y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．画出数轴，把下列各数分别在数轴上表示出来，并用“＜”连接起来：2，0，-3，|-3.5|，-4$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图所示的正方体，如果把它展开，可以得到（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：
    （1）$\sqrt{3}$×（-$\sqrt{6}$）+|-2$\sqrt{2}$|+（$\frac{1}{2}$）-3
    （2）$\frac{\sqrt{18×12}}{\sqrt{32}}$-$\frac{\sqrt{27}}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE、BD、MN．
    （1）求证：△PMN为等腰直角三角形；
    （2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP，BD分别交于点G、H，请判断①中的结论是否成立，若成立，请证明；若不成立，请说明理由．

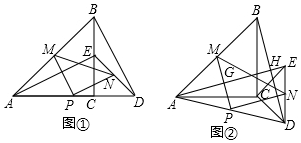
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

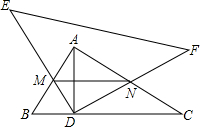    4．如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，AD是BC边上的高，以D为直角顶点的Rt△DEF绕点旋转，在旋转过程中，DE、EF分别与边AB、AC交于点M、N，则线段MN的最大值与最小值的差为$\frac{16}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，在长为6m，宽为4m的矩形地面上修建两条宽均为1m的道路，余下部分做为耕地，根据图中数据，计算耕地面积为15m2．

    查看答案和解析>>

    同步练习册答案