
ЁОЬтФПЁПЮвЪаФГЯчеђЪЕЪЉВњвЕОЋзМЗіЦЖЃЌАяжњЦЖРЇЛЇГаАќСЫШєИЩФЖЭСЕижжжВаТЦЗВннЎЃЌвбжЊИУВннЎЕФГЩБОЮЊУПЧЇПЫ10дЊЃЌВннЎГЩЪьКѓЭЖШыЪаГЁЯњЪлЃЌОЪаГЁЕїВщЗЂЯжЃЌВннЎЯњЪлВЛЛсПїБОЃЌЧвУПЬьЕФЯњЪлСПyЃЈЧЇПЫЃЉгыЯњЪлЕЅМлxЃЈдЊ/ЧЇПЫЃЉжЎМфКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
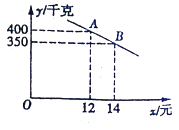
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЕБИУЦЗжжВннЎЕФЖЈМлЮЊЖрЩйЪБЃЌУПЬьЯњЪлЛёЕУРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉФГДхНёФъВннЎВЩеЊЦкЯо30ЬьЃЌдЄМЦВњСП6000ЧЇПЫЃЌдђАДееЃЈ2ЃЉжаЕФЗНЪННјааЯњЪлЃЌФмЗёЯњЪлЭъетХњВннЎЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=-25x+700ЃЈ10ЁмxЁм28ЃЉЃЛЃЈ2ЃЉИУЦЗжжВннЎЖЈМлЮЊ19дЊ/ЧЇПЫЪБЃЌУПЬьЯњЪлЛёЕУЕФРћШѓзюДѓЃЌЮЊ2025дЊЃЛЃЈ3ЃЉФмЯњЪлЭъетХњВннЎЃЌРэгЩМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтПЩЕУНсТлЃЛ
ЃЈ2ЃЉИљОнЁАзмРћШѓ=ЕЅИіРћШѓЁСЯњЪлСПЁБСаГіКЏЪ§НтЮіЪНЃЌВЂХфЗНГЩЖЅЕуЪНМДПЩЕУГізюДѓжЕЃЛ
ЃЈ3ЃЉЧѓГідкЃЈ2ЃЉжаЧщПіЯТЃЌМДx=19ЪБУПЬьЕФЯњЪлСПЃЌОнДЫЧѓЕУ30ЬьЕФзмЯњЪлСПЃЌБШНЯМДПЩЕУГіД№АИЃЎ
ЃЈ1ЃЉЩшyгыxЕФКЏЪ§ЙиЯЕЪНЮЊy=kx+bЃЈkЁй0ЃЉЃЌАбAЃЈ12ЃЌ400ЃЉЃЌBЃЈ14ЃЌ350ЃЉЗжБ№ДњШыЕУ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЁрyгыxЕФКЏЪ§ЙиЯЕЪНЮЊy=-25x+700ЃЌгЩЬтвтжЊЃК
ЃЌЁрyгыxЕФКЏЪ§ЙиЯЕЪНЮЊy=-25x+700ЃЌгЩЬтвтжЊЃК![]() ЃЌЁр10ЁмxЁм28ЃЛ
ЃЌЁр10ЁмxЁм28ЃЛ
ЃЈ2ЃЉЩшУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЌгЩЬтвтжЊw=ЃЈx-10ЃЉЃЈ-25x+700ЃЉ=-25x2+950x-7000 =-25ЃЈx-19ЃЉ2+2025ЃЎ
Ёпa=-25ЃМ0ЃЌЁрЕБx=19ЪБЃЌwШЁзюДѓжЕЃЌЮЊ2025ЃЎ
ЕБИУЦЗжжВннЎЖЈМлЮЊ19дЊ/ЧЇПЫЪБЃЌУПЬьЯњЪлЛёЕУЕФРћШѓзюДѓЃЌЮЊ2025дЊЃЎ
ЃЈ3ЃЉФмЯњЪлЭъетХњВннЎЃЎРэгЩШчЯТЃК
ЕБx=19ЪБЃЌy=-25ЁС19+700=225ЃЌ225ЁС30=6750ЃО6000ЃЎ
ЁрАДееЃЈ2ЃЉжаЕФЗНЪННјааЯњЪлЃЌФмЯњЪлЭъЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪадкШЋУёНЁЩэЛюЖЏжазМБИЮЊЧрЩйФъОйаавЛДЮЭјЧђжЊЪЖНВзљЃЌаЁУїКЭУУУУЖМЪЧЭјЧђУдЃЌвЊЧѓАжАжШЅТђУХЦБЃЌЕЋАжАжжЛТђЛивЛеХУХЦБЃЌФЧУДЫШЅОЭГЩСЫЮЪЬтЃЌаЁУїЯыЕНвЛИіАьЗЈЃКЭЈЙ§зігЮЯЗОіЖЈЫШЅЃЎгЮЯЗЙцдђЪЧЃКдкВЛЭИУїЕФПкДќжаЗжБ№ЗХШы2ИіАзЩЋКЭ1ИіЛЦЩЋЕФЦЙХвЧђЃЌЫќУЧГ§беЩЋЭтЦфгрЖМЯрЭЌЃЎгЮЯЗЪБЯШгЩУУУУДгПкДќжаШЮвтУўГі1ИіЦЙХвЧђМЧЯТбеЩЋКѓЗХЛиВЂвЁдШЃЌдйгЩаЁУїДгПкДќжаУўГі1ИіЦЙХвЧђЃЌМЧЯТбеЩЋЃЎШчЙћНуЕмЖўШЫУўЕНЕФЦЙХвЧђбеЩЋЯрЭЌЃЌдђУУУУгЎЃЌЗёдђаЁУїгЎЃЎ
ЂХ ЧыгУЪїзДЭМЛђСаБэЕФЗНЗЈБэЪОгЮЯЗжаЫљгаПЩФмГіЯжЕФНсЙћЃЎ
ЂЦ етИігЮЯЗЙцдђЖдгЮЯЗЫЋЗНЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЕФжБОЖABЃН26ЃЌPЪЧABЩЯ(ВЛгыЕуAЁЂBжиКЯ)ЕФШЮвЛЕуЃЌЕуCЁЂDЮЊЁбOЩЯЕФСНЕуЃЌШєЁЯAPDЃНЁЯBPCЃЌдђГЦЁЯCPDЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЎ
(1)ШєЁЯBPCЃНЁЯDPCЃН60ЁуЃЌдђЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБТ№ЃПВЂЫЕУїРэгЩЃЛ
(2)Шє![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ІаЃЌЧѓЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃЛ
ІаЃЌЧѓЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃЛ
(3)ШєжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌЧвЁїPCDЕФжмГЄЮЊ24+13![]() ЃЌжБНгаДГіAPЕФГЄЃЎ
ЃЌжБНгаДГіAPЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЁбOЕФФкНгШ§НЧаЮЃЌABЪЧЁбOЕФжБОЖЃЌOFЁЭABЃЌНЛACгкЕуFЃЌЕуEдкABЕФбгГЄЯпЩЯЃЌЩфЯпEMОЙ§ЕуCЃЌЧвЁЯACE+ЁЯAFOЃН180ЁуЃЎ
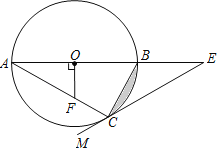
ЃЈ1ЃЉЧѓжЄЃКEMЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁЯAЃНЁЯEЃЌЁбOЕФАыОЖЮЊ1ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЙ§Еу
ЩЯЃЌЙ§Еу![]() зї
зї![]() жсНЛ
жсНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊжБНЧЯюЕуЃЌ
ЮЊжБНЧЯюЕуЃЌ![]() ЮЊжБНЧБпдк
ЮЊжБНЧБпдк![]() ЕФгвВрзїЕШбќжБНЧ
ЕФгвВрзїЕШбќжБНЧ![]() ЃЌдйЙ§Еу
ЃЌдйЙ§Еу![]() зї
зї![]() ЃЌЗжБ№НЛжБЯп
ЃЌЗжБ№НЛжБЯп![]() КЭ
КЭ![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌвдЕу
СНЕуЃЌвдЕу![]() ЮЊжБНЧЖЅЕуЃЌ
ЮЊжБНЧЖЅЕуЃЌ![]() ЮЊжБНЧБпдк
ЮЊжБНЧБпдк![]() ЕФгвВрзїЕШбќжБНЧ
ЕФгвВрзїЕШбќжБНЧ![]() ЃЌЁЃЌАДДЫЙцТЩНјааЯТШЅЃЌдђЕу
ЃЌЁЃЌАДДЫЙцТЩНјааЯТШЅЃЌдђЕу![]() ЕФзјБъЮЊ__________ (НсЙћгУКЌе§ећЪ§
ЕФзјБъЮЊ__________ (НсЙћгУКЌе§ећЪ§![]() ЕФДњЪ§ЪНБэЪО)ЃЎ
ЕФДњЪ§ЪНБэЪО)ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖЏЕу![]() ДгЃЈ0ЃЌ3ЃЉГіЗЂЃЌби
ДгЃЈ0ЃЌ3ЃЉГіЗЂЃЌби![]() жсвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЯТвЦЖЏЃЌЭЌЪБЖЏЕу
жсвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЯТвЦЖЏЃЌЭЌЪБЖЏЕу![]() Дг
Дг![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() жсвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгввЦЖЏЃЌЕБЕу
жсвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгввЦЖЏЃЌЕБЕу![]() вЦЖЏЕН
вЦЖЏЕН![]() ЕуЪБЃЌЕу
ЕуЪБЃЌЕу![]() ЁЂ
ЁЂ![]() ЭЌЪБЭЃжЙвЦЖЏЃЎЕу
ЭЌЪБЭЃжЙвЦЖЏЃЎЕу![]() дкЕквЛЯѓЯоФкЃЌдк
дкЕквЛЯѓЯоФкЃЌдк![]() ЁЂ
ЁЂ![]() вЦЖЏЙ§ГЬжаЃЌЪМжега
вЦЖЏЙ§ГЬжаЃЌЪМжега![]() ЃЌЧв
ЃЌЧв![]() ЃЎдђдкећИівЦЖЏЙ§ГЬжаЃЌЕу
ЃЎдђдкећИівЦЖЏЙ§ГЬжаЃЌЕу![]() вЦЖЏЕФТЗОЖГЄЮЊЃЈ ЃЉ
вЦЖЏЕФТЗОЖГЄЮЊЃЈ ЃЉ
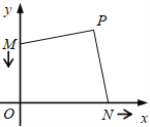
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=Љx2+bx+cЩЯВПЗжЕуЕФКсзјБъxЃЌзнзјБъyЕФЖдгІжЕШчЯТБэЫљЪОЃК
x | Ё | Љ2 | Љ1 | 0 | 1 | 2 | Ё |
y | Ё | 0 | 4 | 6 | 6 | 4 | Ё |
ДгЩЯБэПЩжЊЃЌЯТСаЫЕЗЈжаЃЌДэЮѓЕФЪЧЃЈ ЃЉ
A. ХзЮяЯпгкxжсЕФвЛИіНЛЕузјБъЮЊЃЈЉ2ЃЌ0ЃЉ
B. ХзЮяЯпгыyжсЕФНЛЕузјБъЮЊЃЈ0ЃЌ6ЃЉ
C. ХзЮяЯпЕФЖдГЦжсЪЧжБЯпx=0
D. ХзЮяЯпдкЖдГЦжсзѓВрВПЗжЪЧЩЯЩ§ЕФ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгаЫФеХБГУцЭъШЋЯрЭЌЕФжНХЦ![]() ЃЌЦфе§УцЗжБ№ЛгаЫФИіВЛЭЌЕФМИКЮЭМаЮЃЌНЋетЫФеХжНХЦБГУцГЏЩЯЯДдШ.
ЃЌЦфе§УцЗжБ№ЛгаЫФИіВЛЭЌЕФМИКЮЭМаЮЃЌНЋетЫФеХжНХЦБГУцГЏЩЯЯДдШ.
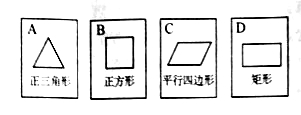
ЃЈ1ЃЉДгжаЫцЛњУўГівЛеХЃЌЧѓУўГіЕФХЦУцЭМаЮЪЧжааФЖдГЦЭМаЮЕФИХТЪЃЛ
ЃЈ2ЃЉаЁУїКЭаЁССдМЖЈзівЛИігЮЯЗЃЌЦфЙцдђЮЊЃКЯШгЩаЁУїЫцЛњУўГівЛеХжНХЦЃЌВЛЗХЛиЃЌдйгЩаЁССДгЪЃЯТЕФжНХЦжаЫцЛњУўГівЛеХЃЌШєУўГіЕФСНеХХЦУцЭМаЮЖМЪЧжсЖдГЦЭМаЮаЁУїЛёЪЄЃЌЗёдђаЁССЛёЪЄЃЌетИігЮЯЗЙЋЦНТ№ЃПЧыгУСаБэЗЈЃЈЛђЪїзДЭМЃЉЫЕУїРэгЩЃЈжНХЦгУ![]() БэЪОЃЉ.
БэЪОЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCжаЃЌЁЯBAC=90ЁуЃЌгУГпЙцЙ§ЕуAзївЛЬѕжБЯпЃЌЪЙЦфНЋЁїABCЗжГЩСНИіЯрЫЦЕФШ§НЧаЮЃЌЦфзїЗЈВЛе§ШЗЕФЪЧ_______ЃЎЃЈЬюађКХЃЉ
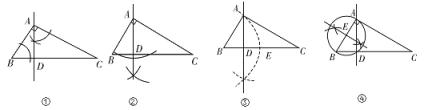
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com