
【题目】抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.

(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
【答案】(1)(1,﹣4);(2)点M坐标为(![]() ,﹣
,﹣![]() )或(5,12).
)或(5,12).
【解析】试题分析:(1)解方程![]() 求出
求出![]() 或
或![]() 抛物线
抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点A在点B左侧),确定点
两点(点A在点B左侧),确定点![]() 的坐标为
的坐标为![]() 将
将![]() 配方,写成顶点式为
配方,写成顶点式为![]() 即可确定顶点
即可确定顶点![]() 的坐标;
的坐标;
(2)①根据抛物线![]() 得到点C、点E的坐标.连接BC,过点C作
得到点C、点E的坐标.连接BC,过点C作![]() 于H,由勾股定理得出
于H,由勾股定理得出![]() 证明
证明![]() 为直角三角形.
为直角三角形.
分别延长![]() 与
与![]() 轴相交于点
轴相交于点![]() 根据两角对应相等的两三角形相似证明
根据两角对应相等的两三角形相似证明![]()
![]() 得出
得出![]() 运用待定系数法求出直线CQ的解析式为
运用待定系数法求出直线CQ的解析式为![]() y=-直线BD的解析式为
y=-直线BD的解析式为![]() 解方程组
解方程组 即可求出点P的坐标;
即可求出点P的坐标;
②分两种情况进行讨论:(Ⅰ)当点M在对称轴右侧时.若点N在射线CD上,如备用图1,延长MN交y轴于点F,过点M作![]() 轴于点G,先证明
轴于点G,先证明![]() 由相似三角形对应边成比例得出
由相似三角形对应边成比例得出![]() .设
.设![]() ,再证明
,再证明![]() 均为等腰直角三角形,然后用含
均为等腰直角三角形,然后用含![]() 的代数式表示点M的坐标,将其代入抛物线
的代数式表示点M的坐标,将其代入抛物线![]() 求出
求出![]() 的值,得到点M的坐标;若点N在射线DC上,同理可求出点M的坐标;(Ⅱ)当点M在对称轴左侧时.由于
的值,得到点M的坐标;若点N在射线DC上,同理可求出点M的坐标;(Ⅱ)当点M在对称轴左侧时.由于![]() 得到
得到![]() 根据直角三角形两锐角互余得出
根据直角三角形两锐角互余得出![]() 而抛物线左侧任意一点K,都有
而抛物线左侧任意一点K,都有![]() 所以点M不存在.
所以点M不存在.
试题解析:
(1)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点A在点B左侧),
两点(点A在点B左侧),
∴当![]() 时,
时,
![]()
解得![]() 或
或![]()
∴点B的坐标为![]()
![]()
∴顶点D的坐标为![]()
(2)①如右图.
∵抛物线![]() 与与y轴交于点C,
与与y轴交于点C,
∴C点坐标为![]()
∵对称轴为直线![]()
∴点E的坐标为![]()
连接BC,过点C作![]() 于H,则H点坐标为
于H,则H点坐标为![]()
![]()
![]()
![]()
![]() 为直角三角形.
为直角三角形.
分别延长![]() 与
与![]() 轴相交于点
轴相交于点![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 即
即![]()
∴直线CQ的解析式为![]()
直线BD的解析式为![]()
由方程组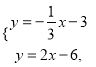 解得
解得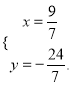 .
.
∴点P的坐标为![]()
②(Ⅰ)当点M在对称轴右侧时.
若点![]() 在射线
在射线![]() 上,如备用图1,延长MN交
上,如备用图1,延长MN交![]() 轴于点F,过点M作
轴于点F,过点M作![]() 轴于点
轴于点![]() .
.
![]()
![]()
![]()
![]()
设![]() 则
则![]()
![]()
![]() 均为等腰直角三角形,
均为等腰直角三角形,
![]()
![]()
![]()
![]()
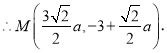
代入抛物线![]() 解得
解得![]()
![]()
若点N在射线DC上,如备用图2,MN交y轴于点F,过点M作![]() 轴于点G.
轴于点G.
![]()
![]()
![]()
![]()
设![]() 则
则![]()
![]()
![]() 均为等腰直角三角形,
均为等腰直角三角形,
![]()
![]()
![]()
![]()
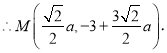
代入抛物线![]() 解得
解得![]()
代入抛物线![]() ,解得
,解得![]()
![]()
(Ⅱ)当点M在对称轴左侧时.
![]()
![]()
而抛物线左侧任意一点K,都有![]()
∴点M不存在.
综上可知,点M坐标为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,我们把横坐标、纵坐标都是整数的点称为整点![]() 如图,直线
如图,直线![]() 和反比例函数
和反比例函数![]() 的图象交于
的图象交于![]() 两点,则落在图中阴影部分
两点,则落在图中阴影部分![]() 不包含边界
不包含边界![]() 内的整点个数有
内的整点个数有![]() 个.
个.

A. 2
B. 3
C. 4
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中: ①abc<0;②4ac﹣b2>0;③a﹣b+c>2;④a<b<0;⑤ac+2=b,
正确的个数有________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所属的集合内:5.2,0,![]() ,
,![]() ,+(﹣4),﹣2
,+(﹣4),﹣2![]() ,﹣(﹣3 ),0.25555…,﹣0.030030003…
,﹣(﹣3 ),0.25555…,﹣0.030030003…
(1)分数集合:{_________________________________________ …}
(2)非负整数集合:{_________________________________________ …}
(3)有理数集合:{_________________________________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解方程:x4﹣6x2+5=0.这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2﹣6y+5=0…①,
解这个方程得:y1=1,y2=5.
当y=1时,x2=1,∴x=±1;
当y=5时,x2=5,∴x=±![]()
所以原方程有四个根:x1=1,x2=﹣1,x3=![]() ,x4=﹣
,x4=﹣![]() .
.
在这个过程中,我们利用换元法达到降次的目的,体现了转化的数学思想.
(1)解方程(x2﹣x)2﹣4(x2﹣x)﹣12=0时,若设y=x2﹣x,则原方程可转化为 ;求出x
(2)利用换元法解方程:![]() =2.
=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
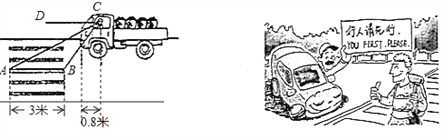
【题目】我国![]() 道路交通安全法
道路交通安全法![]() 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行” ![]() 如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是![]() 和
和![]() ,如果斑马线的宽度是
,如果斑马线的宽度是![]() 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是![]() 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一次函数y1=-x-2与y2=x-4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=-x-2与y2=x-4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1>y2时x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com