
阅读下列材料:
问题:如图1,在□ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线
EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理使
问题得到解决.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.
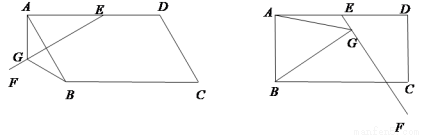
图1 图2
(1)证明见解析
(2)EG=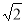 AG﹣BG;证明见解析
AG﹣BG;证明见解析
【解析】
试题分析:(1)作∠GAH=∠EAB交GE于点H,则∠GAB=∠HAE,先根据ASA定理得出△ABG≌△AEH,由∠GAH=∠EAB=60°可知△AGH是等边三角形,故可得出结论;
(2)作∠GAH=∠EAB交GE的延长线于点H,先根据ASA定理得出△ABG≌△AEH,故可得出BG=EH,AG=AH,根据∠GAH=∠EAB=90°可知△AGH是等腰直角三角形,所以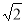 AG=HG,由此可得出结论.
AG=HG,由此可得出结论.
试题解析:(1)如图1,作∠GAH=∠EAB交GE于点H,则∠GAB=∠HAE.
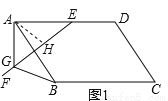
∵∠EAB=∠EGB,∠GAB=∠HAE,
∴∠ABG=∠AEH.
∵又∵AB=AE,
∴△ABG≌△AEH(ASA).
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=60°,
∴△AGH是等边三角形.
∴AG=HG.
∴EG=AG+BG;
(2)线段EG、AG、BG之间的数量关系是EG=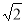 AG﹣BG.
AG﹣BG.
理由如下:
如图2,作∠GAH=∠EAB交GE的延长线于点H,则∠GAB=∠HAE.
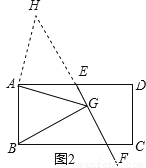
∵∠EGB=∠EAB=90°,
∴∠ABG+∠AEG=∠AEG+∠AEH=180°.
∴∠ABG=∠AEH.
又∵AB=AE,
∴△ABG≌△AEH(ASA).
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=90°,
∴△AGH是等腰直角三角形.
∴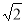 AG=HG,
AG=HG,
∴EG=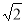 AG﹣BG.
AG﹣BG.
考点:1、全等三角形的判定与性质;2、直角三角形的性质;3、勾股定理


科目:初中数学 来源:2015届天津市河西区八年级下学期期末考试数学试卷(解析版) 题型:填空题
要组织一次排球邀请赛,参赛的每两个各队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?若设应邀请x各队参赛,可列出的方程为 _________ .
查看答案和解析>>
科目:初中数学 来源:2015届北京市顺义区八年级下学期期末考试数学试卷(解析版) 题型:选择题
已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是( )
A.3 B.4 C.6 D.5
查看答案和解析>>
科目:初中数学 来源:2015届北京市门头沟区八年级下学期期末考试数学试卷(解析版) 题型:解答题
某校数学兴趣小组的成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图.

请你根据图表提供的信息,解答下列问题:
(1)频数分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是 .
查看答案和解析>>
科目:初中数学 来源:2015届北京市昌平区八年级下学期期末考试数学试卷(解析版) 题型:解答题
【问题提出】如果我们身边没有量角器和三角板,如何作15°大小的角呢?
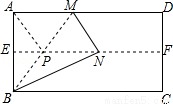
【实践操作】如图.
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开,得到AD∥EF∥BC.
第二步:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM.折痕BM 与折痕EF相交于点P.连接线段BN,PA,得到PA=PB=PN.
【问题解决】
(1)求∠NBC的度数;
(2)通过以上折纸操作,还得到了哪些不同角度的角?请你至少再写出两个(除∠NBC的度数以外).
(3)你能继续折出15°大小的角了吗?说说你是怎么做的.
查看答案和解析>>
科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:选择题
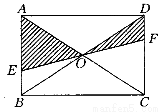
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的( ).
A.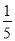 B.
B.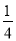 C.
C.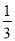 D.
D.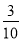
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com