
科目: 来源: 题型:
【题目】某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,与AB、AC分别相交于E、F,若已知AB=9,AC=7,求△AEF的周长.
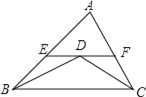
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() =
=![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数0对应的点之间的距离;这个结论可以推广为
与数0对应的点之间的距离;这个结论可以推广为![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离;
对应的点之间的距离;
例1.解方程|![]() |=2.因为在数轴上到原点的距离为2的点对应的数为
|=2.因为在数轴上到原点的距离为2的点对应的数为![]() ,所以方程|
,所以方程|![]() |=2的解为
|=2的解为![]() .
.
例2.解不等式|![]() -1|>2.在数轴上找出|
-1|>2.在数轴上找出|![]() -1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|
-1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|![]() -1|=2的解为
-1|=2的解为![]() =-1或
=-1或![]() =3,因此不等式|
=3,因此不等式|![]() -1|>2的解集为
-1|>2的解集为![]() <-1或
<-1或![]() >3.
>3.
![]()
例3.解方程|![]() -1|+|
-1|+|![]() +2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的
+2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的![]() 的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的
的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的![]() 对应的点在1的右边或-2的左边.若
对应的点在1的右边或-2的左边.若![]() 对应的点在1的右边,可得
对应的点在1的右边,可得![]() =2;若
=2;若![]() 对应的点在-2的左边,可得
对应的点在-2的左边,可得![]() =-3,因此方程|
=-3,因此方程|![]() -1|+|
-1|+|![]() +2|=5的解是
+2|=5的解是![]() =2或
=2或![]() =-3.
=-3.
![]()
参考阅读材料,解答下列问题:
(1)方程|![]() +3|=4的解为 ;
+3|=4的解为 ;
(2)解不等式:|![]() -3|≥5;
-3|≥5;
(3)解不等式:|![]() -3|+|
-3|+|![]() +4|≥9
+4|≥9
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点. 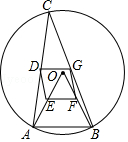
(1)试判断四边形DEFG的形状,并说明理由;
(2)填空: ①若AB=3,当CA=CB时,四边形DEFG的面积是;
②若AB=2,当∠CAB的度数为时,四边形DEFG是正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: 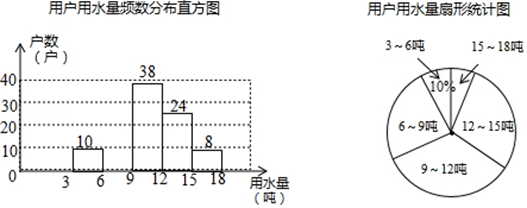
(1)此次抽样调查的样本容量是;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.
(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:BM=CN;
②如图2,当点M运动到线段BC之外时,其它条件不变,①中结论BM=CN还成立吗?请说明理由.
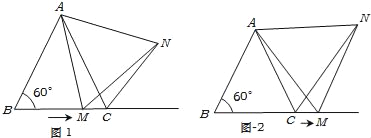
查看答案和解析>>
科目: 来源: 题型:
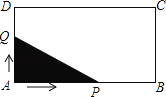
【题目】如图,长方形ABCD中,AB=8,AD=4.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com