【题目】如图所示，已知直线的图象与x轴、y轴交于A，B两点，直线经过原点，与线段AB交于点C，把的面积分为2：1的两部分，求直线的解析式．

【题目】如图，四边形ABCD中，，，，垂足为E.求证：．

【题目】把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F重合（E、F两点均在BD上），折痕分别为BH、DG．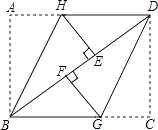
（1）求证：△BHE≌△DGF；
（2）若AB=6cm，BC=8cm，求线段FG的长．

【题目】第六次全国人口普查工作圆满结束，2011年5月20日《遵义晚报》报到了遵义市人口普查结果，并根据我市常住人口情况，绘制出不同年龄的扇形统计图；普查结果显示，2010年我市常住人口中，每10万人就有4402人具有大学文化程度，与2000年第五次人口普查相比，是2000年每10万人具有大学文化程度人数的3倍少473人，请根据以上信息，解答下列问题．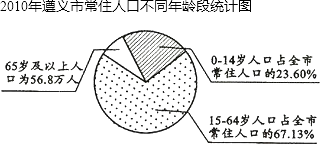
（1）65岁及以上人口占全市常住人口的百分比是；
（2）我市2010年常住人口约为万人（结果保留四个有效数字）；
（3）与2000年我市常住人口654.4万人相比，10年间我市常住人口减少万人；
（4）2010年我市每10万人口中具有大学文化程度人数比2000年增加了多少人？

【题目】在数、、、、…、、的每个数字前添上“+”或“-”，使得算出的结果是一个最小的非负数，请写出符合条件的式子：________．

【题目】如图，在中，，BD为AC的中线，过点C作于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接 BG，DF．若AF=8，CF=6，则四边形BDFG的周长为_______________．

【题目】某市为缓解城市交通压力，决定修建人行天桥，原设计天桥的楼梯长AB=6m，∠ABC=45°，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使∠ADC=30°（如图所示）．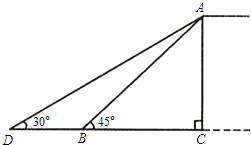

（结果保留根号）
（1）求调整后楼梯AD的长；
（2）求BD的长．

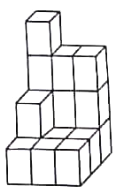
【题目】如图，在一次数学活动课上，张明用17个底面为正方形，且底面边长为，高为的小长方体达成了一个几何体，然后他请王亮用尽可能少的同样的长方体在旁边再搭一个几何体，使王亮所搭的几何体恰好可以和张明所搭的几何体拼成一个大长方体（即拼大长方体时将其中一个几何体翻转，且假定组成每个几何体的小长方体粘合在一起）.

（1）王亮至少还需要 个小长方体；

（2）请画出张明所搭几何体的左视图，并计算它的表面积（用含的代数式表示）；

（3）请计算（1）条件下王亮所搭几何体的表面积（用含的代数式表示）.

【题目】菱形OABC在平面直角坐标系中的位置如图所示顶点A（5,0），OB=，P是对角线OB上的一个动点，D（0,1），当CP+DP的值最小时，点P的坐标为（　　）

A. (，3) B. （，） C. （1，） D. （，）

（1）应用一：已知点A在数轴上表示为，数轴上任意一点B表示的数为，则AB两点的距离可以表示为 ；应用这个知识，请写出当 时，有最小值为 .

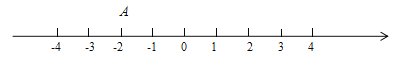
（2）应用二：从数轴上取下一个单位长度的线段，第一次剪掉原长的，第二次剪掉剩下的，依次类推，每次都剪掉剩下的，则剪掉5次后剩下线段长度为 ；应用这个原理，请计算：.

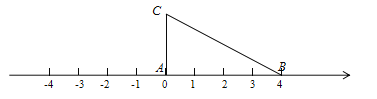
（3）应用三：如图，将一根拉直的细线看作数轴，一个三边长分别为的三角形的顶点与原点重合，边在数轴正半轴上，将数轴正半轴的线沿的顺序依次缠绕在三角形的边上，负半轴的线沿的顺序依次缠绕在三角形的边上.

①如果正半轴的线缠绕了5圈，负半轴的线缠绕了3圈，求绕在点上的所有数之和；

②如果正半轴的线不变，将负半轴的线拉长一倍，即原线上的点的位置对应着拉长后的数，并将三角形向正半轴平移一个单位后再开始绕，求绕在点且绝对值不超过100的所有数之和.