科目： 来源： 题型：
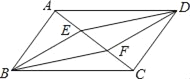
【题目】如图，在□ABCD中，E，F是对角线AC上的两点且AE=CF，在①BE=DF；②BE∥DF；③AB=DE；④四边形EBFD为平行四边形；⑤S△ADE=S△ABE；⑥AF=CE这些结论中正确的是_____．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S1、S2、S3、S4．则S1+S2+S3+S4等于（ ）
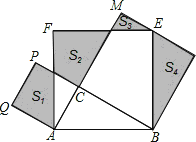
A．14 B．16 C．18 D．20
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC、BC边上运动，且保持AD=CE，连接DE，DF，EF，在此运动过程中，下列结论：（1）△DFE是等腰直角三角形；（2）DE长度的最小值为4；（3）四边形CDFE的面积保持不变；（4）△CDE面积的最大值是4．正确的结论是（ ）
A. （1）（2）（3） B. （1）（3）（4） C. （1）（2）（4） D. （2）（3）（4）
查看答案和解析>>
科目： 来源： 题型：
【题目】已知：平面直角坐标系中，A(a，3)、B(b，6)、C(c，1)，a、b、c都为实数，并且满足3b－5c＝－2a－18，4b－c＝3a＋10
(1) 请直接用含a的代数式表示b和c
(2) 当实数a变化时，判断△ABC的面积是否发生变化？若不变，求其值；若变化，求其变化范围
(3) 当实数a变化时，若线段AB与y轴相交，线段OB与线段AC交于点P，且S△PAB＞S△PBC，求实数a的取值范围.
查看答案和解析>>
科目： 来源： 题型：
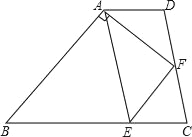
【题目】如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，点F是CD的中点，且AF⊥AB，若AD=2.7，AF=4，AB=6，则CE的长为（ ）
A. 2
B. 2
-1 C. 2.5 D. 2.3
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在平面直角坐标系
中,直线
经过点
且与直线
：
平行，直线与
轴、
轴分别交于点B、C.
（1）求直线l1的表达式及其与轴的交点D的坐标；
（2）判断四边形ABCD是什么四边形？并证明你的结论；
（3）若点E是直线AB上一点，平面内存在一点F，使得四边形CBEF是正方形，求点E的坐标，请直接写出答案.
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，∠AEF＝80°，且∠A＝x°，∠C＝y°，∠F＝z°．若
＋|y－80－m|＋|z－40|＝0（m为常数，且0＜m＜100）
(1) 求∠A、∠C的度数（用含m的代数式表示）
(2) 求证：AB∥CD
(3) 若∠A＝40°，∠BAM＝20°，∠EFM＝10°，直线AM与直线FM交于点M，直接写出∠AMF的度数
查看答案和解析>>
科目： 来源： 题型：
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机，若购进2部甲型号手机和1部乙型号手机，共需要资金2800元；若购进3部甲型号手机和2部乙型号手机，共需要资金4600元
(1) 求甲、乙型号手机每部进价为多少元？
(2) 该店计划购进甲、乙两种型号的手机销售，预计用不多于1.8万元且不少于1.74万元的资金购进这两部手机共20台，请问有几种进货方案？请写出进货方案
(3) 售出一部甲种型号手机，利润率为40%，乙型号手机的售价为1280元．为了促销，公司决定每售出一台乙型号手机，返还顾客现金m元，而甲型号手机售价不变，要使(2)中所有方案获利相同，求m的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
