
科目: 来源: 题型:
【题目】丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
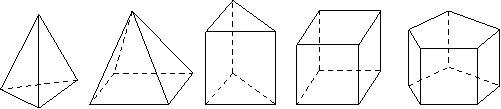
观察:下面这些几何体都是简单几何体,请您仔细观察.
![]()
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体 | a | b | c | d | e |
棱数(E) | 6 | 9 | 15 | ||
面数(F) | 4 | 5 | 5 | 6 | |
顶点数(V) | 4 | 5 | 8 |
发现:(1)简单几何中,![]() ;
;
(2)简单几何中,每条棱都是 个面的公共边;
(3)在正方体中,每个顶点处有 条棱,每条棱都有 个顶点,所以有2![]() 3
3![]() .
.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有 条棱, 个顶点,每个顶点处有 条棱.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】在一次设计比赛中,小军10次射击的成绩是:6环1次,7环3次,8环2次,9环3次,10环1次,关于他的射击成绩,下列说法正确的是( )
A.极差是2环
B.中位数是8环
C.众数是9环
D.平均数是9环
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,同时直线PQ由点B出发,沿BA的方向匀速运动,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t≤5).线段CM的长度记作y甲 , 线段BP的长度记作y乙 , y甲和y乙关于时间t的函数变化情况如图所示.
(1)由图2可知,点M的运动速度是每秒 cm,当t为何值时,四边形PQCM是平行四边形?在图2中反映这一情况的点是;
(2)设四边形PQCM的面积为ycm2 , 求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM= ![]() S△ABC?若存在,求出t的值;若不存在,说明理由;
S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.
(1)建立适当的直角坐标系,并写出各个顶点的坐标.
(2)将(1)中各顶点的横坐标不变,将纵坐标都乘-1,与原图案相比,所得的图案有什么变化?
(3)将(1)中各顶点的横坐标都乘-2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
查看答案和解析>>
科目: 来源: 题型:
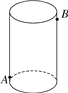
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题: 
(1)探究:若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是;如图2,当a=°时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=(用含有R、m的代数式表示)
(4)拓展:如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 , 并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:数轴上有A、B两点,分别对应的数为a,b,已知(a+1)2与|b﹣3|互为相反数.点P为数轴上一动点,对应为x.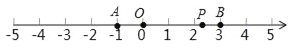
(1)a= ;b=
(2)若点P到点A和点B的距离相等,则点P对应的数是
(3)数轴上是否存在点P,使点P到点A和点B的距离之和为5?若存在,请求出x的值;若不存在,说明理由;
(4)|x﹣a|+|x﹣b|的最小值=
(5)当点P以每分钟1个单位长度的速度从O点向左运动,点A以每分钟5个单位长度向左运动,问几分钟时点P到点A、点B的距离相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com