
科目: 来源: 题型:
【题目】新定义函数:在y关于x的函数中,若0≤x≤1时,函数y有最大值和最小值,分别记ymax和ymin , 且满足 ![]() ,则我们称函数y为“三角形函数”.
,则我们称函数y为“三角形函数”.
(1)若函数y=x+a为“三角形函数”,求a的取值范围;
(2)判断函数y=x2﹣ ![]() x+1是否为“三角形函数”,并说明理由;
x+1是否为“三角形函数”,并说明理由;
(3)已知函数y=x2﹣2mx+1,若对于0≤x≤1上的任意三个实数a,b,c所对应的三个函数值都能构成一个三角形的三边长,则求满足条件的m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制,0.08元/分;
(B)包月制,50元/月(限一部个人住宅电话上网);
此外,每种上网方式都附加通信费0.02元/分.
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况?如果存在,请求出这时的上网时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】重庆市中小学教育大力提倡“2+2”素质教育,在开展的几年来,取得了重大成果.小明对本学期全班50名同学所选择的活动项目进行了统计,根据收集的数据制作了下表:
1)请完善表格中的数据:

2)根据上述表格中的人数百分比,绘制合适的统计图.
查看答案和解析>>
科目: 来源: 题型:
【题目】省希望工程办公室收到社会各界人士捐款共1500万元.以此来资助贫困失学儿童.
(1)如果每名失学儿童可获得500元的资助,那么共可资助多少名失学儿童?用科学记数法表示结果.
(2)如果社会各界人士的捐款数平均为10元/人,则需要多少人捐款才能获得这笔捐款?用科学记数法表示结果.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a与b满足![]() ,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为
,数轴上点A 和点B 所对应的数分别为a和b,点P 为数轴上一动点,其对应的数为![]() .
.
(1)求a,b的值.
(2)若点 P 到点 A、点 B 的距离相等,求点P对应的数.
(3)现在点 A、点 B 分别以 2 个单位长度/秒和 0.5 个单位长度/秒的速度同时向右运动,点 P 以 3 个单位长度/秒的速度同时从原点向左运动.当点 A 与点 B 之间的距离为2个单位长度时,求点 P 所对应的数是多少?
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
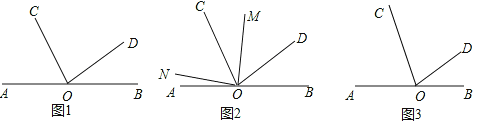
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
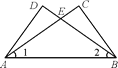
A. ∠DAE=∠CBE B. CE=DE C. △DAE与△CBE不一定全等 D. ∠1=∠2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y= ![]() x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y= ![]() x2+bx+c交于第四象限的F点.
x2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒 ![]() 个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )

A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com