
科目: 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】探索发现:![]() ;
;![]() ;
;![]() …根据你发现的规律,回答下列问题
…根据你发现的规律,回答下列问题
(1)![]() ,
,![]() ;
;
(2)利用你发现的规律计算:![]() ;
;
(3)灵活利用规律解方程:
![]()
【答案】(1) ![]() ,
, ![]() ;(2)
;(2) ![]() (3)100.
(3)100.
【解析】(1)利用分式的运算和题中的运算规律求解;
(2)利用前面的运算规律得到原式=![]() ,然后合并后通分即可;
,然后合并后通分即可;
(3)利用前面的运算规律方程化为![]() ,然后合并后解分式方程即可.
,然后合并后解分式方程即可.
(1)![]() ,
,![]() ; ;
; ;
(2)原式=![]() =
=![]() =
=![]() ;
;
(3) ![]()
![]() ,
,
![]() ,
,
经检验![]() 是原方程的解.
是原方程的解.
点睛:本题考查了分式的运算和解分式方程:熟练掌握解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.理解分式的计算规律:![]() 是解答本题的关键.
是解答本题的关键.
【题型】解答题
【结束】
26
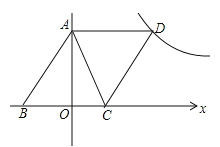
【题目】如图,已知,A(0,6),B(-4.5,0),C(3,0),D为B点关于AC的对称点,反比例函数y= ![]() 的图象经过D点.
的图象经过D点.
(1)点
(2)求此反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
查看答案和解析>>
科目: 来源: 题型:
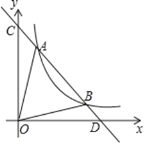
【题目】如图,一次函数![]() 分别交y轴、x轴于C、D两点,与反比例函数y=
分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出![]() <
<![]() 的x的取值范围;
的x的取值范围;
(3)求![]() 的面积.
的面积.
【答案】(1)y=![]() ;(2)
;(2) ![]() 或
或![]() ;(3)15.
;(3)15.
【解析】(1)把B(4,n)两点分别代入![]() 可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
(2)观察函数图象得到当![]() 或
或![]() ,反比例函数的图象在一次函数图象上方.
,反比例函数的图象在一次函数图象上方.
(3)求得直线![]() 与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
(1)将![]() 代入
代入![]() 得
得![]() ,
,
得反比例函数的关系式是![]() .
.
(2)![]() 或
或![]() ,
,
(3)![]() 点的坐标是(0,10),
点的坐标是(0,10),![]() 点的坐标是(5,0),
点的坐标是(5,0),
分别过点A、B两点作![]() 轴、
轴、![]() 轴的垂线段,
轴的垂线段,
![]() .
.
点睛:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及观察图象的能力.
【题型】解答题
【结束】
25
【题目】探索发现:![]() ;
;![]() ;
;![]() …根据你发现的规律,回答下列问题
…根据你发现的规律,回答下列问题
(1)![]() ,
,![]() ;
;
(2)利用你发现的规律计算:![]() ;
;
(3)灵活利用规律解方程:
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目: 来源: 题型:
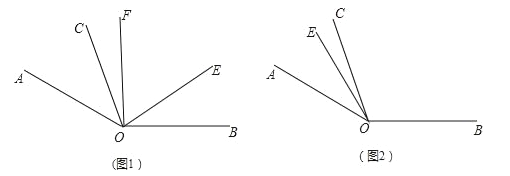
【题目】如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=30°,则∠COF= ;
(2)若∠COF=20°,则∠EOB= ;
(3)若∠COF=n°,则∠EOB= (用含n的式子表示).
(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了构建城市立体道路网络,决定修建一条轻轨铁路,为使工程提前半年完成,需要将工作效率提高25%,原计划完成这项工程需要多少个月?
【答案】原计划完成这项工程需要30个月
【解析】试题设原计划完成这项工程需要x个月,由等量关系“工程提前6个月完成,需将原定的工作效率提高25%”列出方程,求解即可
试题解析:设原计划完成这项工程需要x个月,则有
![]()
解得x=30
经检验x=30是原方程的根
答:原计划完成这项工程需要30个月
考点:分式方程的应用
【题型】解答题
【结束】
24
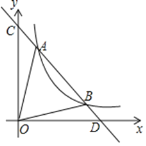
【题目】如图,一次函数![]() 分别交y轴、x轴于C、D两点,与反比例函数y=
分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出![]() <
<![]() 的x的取值范围;
的x的取值范围;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
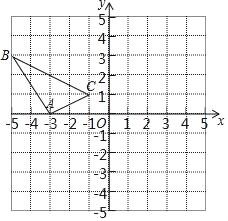
【答案】(1)画图见解析;(2)(0,2).
【解析】
(1)根据中心对称和平移性质分别作出变换后三顶点的对应点,再顺次连接可得;
(2)根据中心对称的概念即可判断.
(1)如图所示,△A1B1C1和△A2B2C2即为所求;
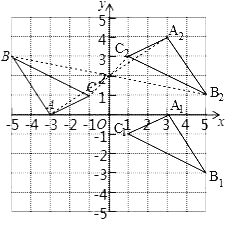
(2)由图可知,△A2B2C2与△ABC关于点(0,2)成中心对称.
点睛:本题考查了中心对称作图和平移作图,熟练掌握中心对称的性质和平移的性质是解答本题的关键. 中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
【题型】解答题
【结束】
22
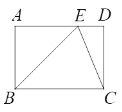
【题目】如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
(2)已知AB=1,∠ABE=45°,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com