【题目】如图，一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等)，则根据图中数据可得原长方体的体积是_________cm3．

【答案】20

【解析】

利用正方形的性质以及图形中标注的长度得出AB=AE=5cm，进而得出长方体的长、宽、高进而得出答案．

如图：

，

∵四边形ABCD是正方形，

∴AB=AE=5cm，

∴立方体的高为：（7-5）÷2=1（cm），

∴EF=5-1=4（cm），

∴原长方体的体积是：5×4×1=20（cm3）．

故答案为：20．

【点睛】

此题主要考查了几何体的展开图，利用已知图形得出各边长是解题关键．

【题型】填空题
【结束】
19

（1）-4-28-(-19)+(-24)；

（2）-14÷(2017-π)0-(-)-2.

【题目】A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行．已知甲车的速度为100千米/时，乙车的速度为80千米/时，___________小时后两车相距30千米．

【答案】或

【解析】

应该有两种情况，第一次应该还没相遇时相距30千米，第二次应该是相遇后交错离开相距30千米，根据路程=速度×时间，可列方程求解．

设第一次相距30千米时，经过了x小时，

由题意，得（100+80）x=450-30，

解得x=；

设第二次相距30千米时，经过了y小时，

由题意，得（100+80）y=450+30，

解得y=，

故经过小时或小时相距30千米．

故答案为：或

【点睛】

本题考查理解题意能力，关键知道相距30千米时有两次以及知道路程=速度×时间，以路程做为等量关系可列方程求解．

【题型】填空题
【结束】
18

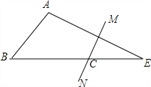
A. 45° B. 60° C. 50° D. 55°

A. 1︰1︰1

B. 1︰2︰3

C. 2︰3︰4

D. 3︰4︰5

【题目】一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x（min）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：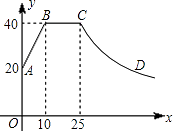
（1）上课后第5min与第30min相比较，何时学生注意力更集中？
（2）某道难题需连续讲19min，为保证效果，学生注意力指数不宜低于36，老师能否在所需要求下讲完这道题？

【题目】如图，某高楼顶部有一信号发射塔，小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β，AD=18m，CD=78m．

（1）用α和β的三角函数表示CE；
（2）当α=30°、β=60°时，求EF（结果精确到1m）．
（参考数据： ≈1.414， ≈1.732）

A. 6个 B. 5个 C. 4个 D. 3个

（1）哪条线表示乙车离出发地的距离y与追赶时间x之间的关系？

（2）甲，乙两车的速度分别是多少？

（3）试分别确定甲，乙两车相对于出发地的距离y（km）与追赶时间x（h）之间的关系式；

（4）乙车能在1.5小时内追上甲车吗？若能，说明理由；若不能，求乙车出发几小时才能追上甲？

【题目】若10m=5，10n=3，则102m+3n=　 　．

【答案】675．

【解析】102m+3n=102m103n=(10m)2(10n)3=5233=675，

故答案为：675.

点睛：此题考查了幂的乘方与积的乘方, 同底数幂的乘法. 首先根据同底数幂的乘法法则，可得102m+3n=102m×103n，然后根据幂的乘方的运算方法，可得102m×103n=（10m）2×（10n）3，最后把10m=5，10n=2代入化简后的算式，求出102m+3n的值是多少即可．

【题型】填空题
【结束】
17

【题目】一个不透明的口袋中装有红、白两种颜色的小球（除颜色外其余都相同），其中红球3个，白球1个．
（1）求任意摸出一球是白球的概率；
（2）甲同学先随机摸出一个小球（不放回），再随机摸出一个小球，请用画树状图或列表的方法求两次摸出都是红球的概率．