
科目: 来源: 题型:
【题目】如图,茬四边形ABCD中,AD∥BC,E是BC的中点,AC平分∠BCD,且AC⊥AB,接DE,交AC于F. 
(1)求证:AD=CE;
(2)若∠B=60°,试确定四边形ABED是什么特殊四边形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市在一次市政施工中,有两段长度相等的人行道铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设人行道的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: 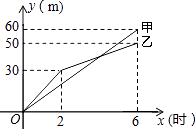
(1)求乙队在2≤x≤6的时间段内,y与x的函数关系式;
(2)若甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完成,所铺设的人行道共是多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
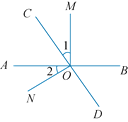
【题目】如图,直线AB,CD相交于点O,过点O作两条射线OM,ON,且∠AOM=∠CON=90°.
(1)若OC平分∠AOM,求∠AOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目: 来源: 题型:
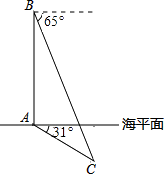
【题目】在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)
(参考数据:sin31°≈ ![]() ,tan31°≈
,tan31°≈ ![]() ,sin65°≈
,sin65°≈ ![]() ,tan65°≈
,tan65°≈ ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目: 来源: 题型:
【题目】随着全国各地空气出现严重污染,PM2.5屡屡爆表,我国多个城市发生雾霾天气,越来越多的人开始关注一个原本陌生的术语﹣PM2.5.某校九年级共有1000名学生,团委准备调查他们对“PM2.5”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案: 方案一:调查九年级部分女生;
方案二:调查九年级部分男生;
方案三:到九年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图,请你根据图中信息,将其补充完整; 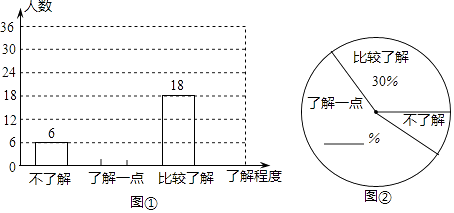
(3)请你估计该校九年级约有多少名学生比较了解“PM2.5”的知识.
查看答案和解析>>
科目: 来源: 题型:
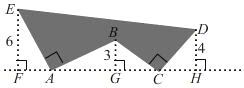
【题目】如图,EF、BG、DH 都垂直于 FH,AE⊥AB 且 AE=AB,BC⊥CD 且 BC=CD,请按照图中所标注的数据,计算图中阴影部分的面积 S 是_____.
查看答案和解析>>
科目: 来源: 题型:
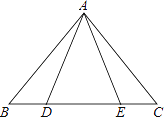
【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com