
科目: 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
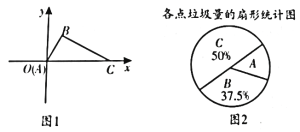
【题目】2017年4月20日,成都举行了“建城市森林,享低碳生活”的垃圾分类推进工作启动仪式,在成都设置有专门的垃圾存放点,做到日产日清。在平面直角坐标系中xOy中,A,B,C三个垃圾存放点的位置如图1所示,点A在原点,![]() ,
,![]() .某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
.某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
(1)若C处的垃圾存放量为320千克,求A处的垃圾存放量。
(2)现需要A,C两处的垃圾分别沿道路AB,CB都运到B处,若点B的横坐标为50,平面直角坐标系中一个单位长度所表示的实际距离是1米,每运送1千克垃圾1米的费用为0.005元,求本次运送垃圾的总费用。(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目: 来源: 题型:
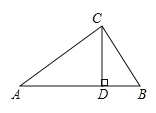
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠ABD=90°,
(1)点B在直线 上,点D在直线 外;
(2)直线 与直线 相交于点A,点D是直线 与直线 的交点,也是直线 与直线 的交点,又是直线 与直线 的交点;
(3)直线 ⊥直线 ,垂足为点 ;
(4)过点D有且只有 条直线与直线AC垂直.
查看答案和解析>>
科目: 来源: 题型:
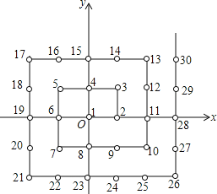
【题目】某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点![]() ,3的对应点是
,3的对应点是![]() ,16的对应点是
,16的对应点是![]() .那么最后一名同学的位置对应的坐标是____,全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是___.
.那么最后一名同学的位置对应的坐标是____,全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com