
科目: 来源: 题型:
【题目】下列条件中,不能判断四边形ABCD是平行四边形的为( )
A. AB∥CD,AD∥BC
B. AB=CD,AD=BC
C. AB∥CD,AD=BC
D. AB∥CD,AB=CD
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)求函数图象的对称轴、顶点坐标、与坐标轴交点的坐标,并画出函数的大致图象;
(2)根据图象直接写出函数值y为负数时,自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】张大伯承包了一个四边形的池塘,如图所示,它的四个角A,B,C,D处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且扩建后的池塘呈平行四边形形状.张大伯这一设想是否能实现?请你帮助他解决一下,并画出草图.
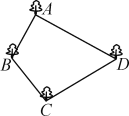
查看答案和解析>>
科目: 来源: 题型:
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解. 根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有个,分别为;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).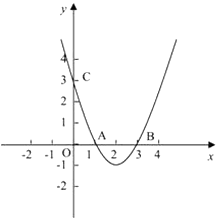
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E. 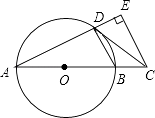
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.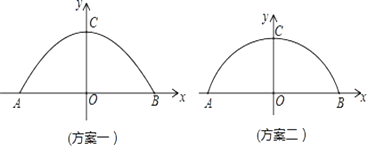
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标分别是点
的坐标分别是点![]() ,
,![]() ,且
,且![]() 满足:
满足:![]() .
.
(1)则![]() _________,
_________,![]() _________;
_________;
(2)![]() 为
为![]() 轴负半轴上一点,过点
轴负半轴上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
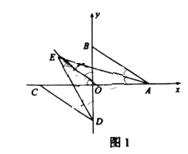
①如图1,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 的度数;
的度数;
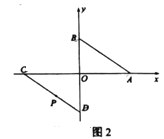
②如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,求
上一点,求![]() 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com