（2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

【题目】如图，已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点，与反比例函数y2=的图象分别交于C、D两点，点D（2，﹣3），点B是线段AD的中点．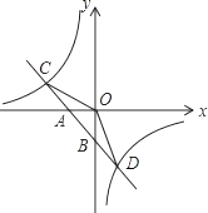

（1）求一次函数y1=k1x+b与反比例函数y2=的解析式；
（2）求△COD的面积；
（3）直接写出 k1x+b≥0 时自变量x的取值范围．
（4）动点P（0，m）在y轴上运动，当 |PCPD| 的值最大时，求点P的坐标．

A.∠A=40°，∠B=50°B.∠A=40°，∠B=60°

C.∠A=20°，∠B=80°D.∠A=40°，∠B=80°

【题目】如图，四边形ABCD为矩形，O为AC中点，过点O作AC的垂线分别交AD、BC于点E、F，连接AF、CE．

（1）求证：四边形AFCE是菱形．
（2）若AC=8，EF=6，求BF的长.

A．2：5 B．14：25 C．16：25 D．4：21

【题目】某超市计划经销一些特产，经销前，围绕“A：王高虎头鸡，B：羊口咸蟹子，C：桂河芹菜，D：巨淀湖咸鸭蛋”四种特产，在全市范围内随机抽取了部分市民进行问卷调查：“我最喜欢的特产是什么？”（必选且只选一种）．现将调查结果整理后，绘制成如图所示的不完整的扇形统计图和条形统计图．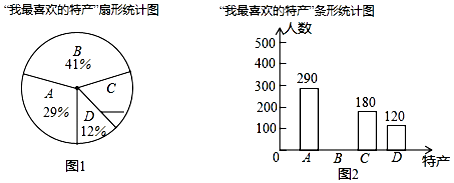
（1）请补全扇形统计图和条形统计图；
（2）若全市有110万市民，估计全市最喜欢“羊口咸蟹子”的市民约有多少万人？
（3）在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球（除标记外完全相同），随机摸出一个小球然后放回，混合摇匀后，再随机摸出一个小球，则两次都摸到A的概率是多少？写出分析计算过程．

斐波那契（约1170﹣1250）是意大利数学家，他研究了一列数，这列数非常奇妙，被称为斐波那契数列（按照一定顺序排列着的一列数称为数列）．后来人们在研究它的过程中，发现了许多意想不到的结果，在实际生活中，很多花朵（如梅花、飞燕草、万寿菊等）的瓣数恰是斐波那契数列中的数．斐波那契数列还有很多有趣的性质，在实际生活中也有广泛的应用．斐波那契数列中的第n个数可以用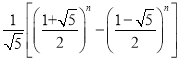表示（其中，n≥1）．这是用无理数表示有理数的一个范例．

任务：请根据以上材料，通过计算求出斐波那契数列中的第1个数和第2个数．

（1）求原计划每天生产的零件个数和规定的天数．

（2）为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%，按此测算，恰好提前两天完成24000个零件的生产任务，求原计划安排的工人人数．

【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.2元，每天可多售出40斤，为保证每天至少售出260斤，张阿姨决定降价销售．
（1）若将这种水果每斤的售价降低x元，则每天的销售量是斤（用含x的代数式表示）；
（2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？