
科目: 来源: 题型:
【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各式从左到右的变形,是因式分解的是()
A.x2-9+6x=(x+3)(x-3)+6xB.(x+5)(x-2)=x2+3x-10
C.x2-8x+16=(x-4)2D.x2+1=x(x+![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为______;
的度数为______;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() .
.
①如图2,若![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示);
的代数式表示);
②如图3,若![]() 绕点
绕点![]() 旋转,分别交线段
旋转,分别交线段![]() 于点
于点![]() ,试问在旋转过程中
,试问在旋转过程中![]() 的度数是否会发生改变?若不变,求出
的度数是否会发生改变?若不变,求出![]() 的度数(用含
的度数(用含![]() 的代数式表示),若改变,请说明理由:
的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线![]() ,与线段
,与线段![]() 交于点
交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系(用含
的关系(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2= ![]() 的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.
的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.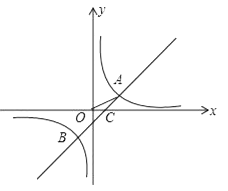
(1)求反比例函数解析式和点B坐标;
(2)当x的取值范围是时,有y1>y2 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )

A. AF=AEB. △ABE≌△AGFC. AF=EFD. BE=3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 的
的![]() 边的异侧作
边的异侧作![]() ,并使
,并使![]() .点
.点![]() 在射线
在射线![]() 上.
上.
(1)如图,若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,试解决下面两个问题:
,试解决下面两个问题:
①如图2,![]() ,求
,求![]() 的度数;
的度数;
②如图3,若![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
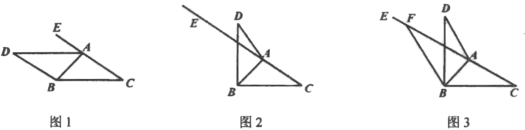
查看答案和解析>>
科目: 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解中学2 000名学生家长对“中学生骑电动车上学”的态度,从中随机调查400名家长,结果有360名家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查
B. 该校只有360名家长持反对态度
C. 样本是360名家长
D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目: 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
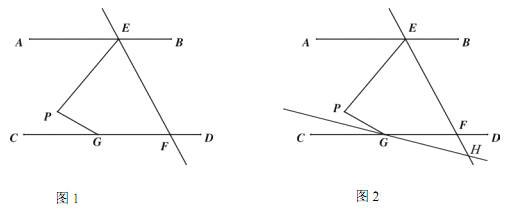
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点A,B分别是x轴正半轴与y轴正半轴上一点,OA=m,OB=n,以AB为边在第一象限内作正方形ABCD.
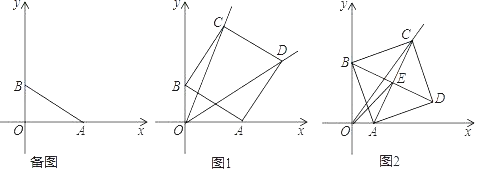
(1)若m=4,n=3,直接写出点C与点D的坐标;
(2)点C在直线y=kx(k>1且k为常数)上运动.
①如图1,若k=2,求直线OD的解析式;
②如图2,连接AC、BD交于点E,连接OE,若OE=2![]() OA,求k的值.
OA,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在四边形ABCD中,点E、点F分别为AD、BC的中点,连接EF.
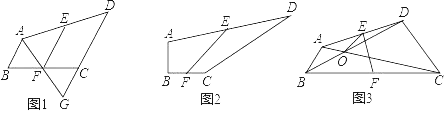
(1)如图1,AB∥CD,连接AF并延长交DC的延长线于点G,则AB、CD、EF之间的数量关系为 ;
(2)如图2,∠B=90°,∠C=150°,求AB、CD、EF之间的数量关系?
(3)如图3,∠ABC=∠BCD=45°,连接AC、BD交于点O,连接OE,若AB=![]() ,CD=2
,CD=2![]() ,BC=6,则OE= .
,BC=6,则OE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com