【题目】已知关于x、y的方程组

（1）求方程组的解（用含a的代数式表示）；

（2）若2x>y,求a的范围；

（3）求代数式的值；

（4）若，求a的值（直接写出结果）．

【题目】计算：|﹣2|﹣2cos60°+（ ）﹣1﹣（π﹣ ）0 ．

【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A，B两点，与y轴交于点C，且OA=OC，则下列结论：①abc＜0；② ；③ac﹣b+1=0；④OAOB=﹣ ．其中正确结论的序号是 ．

【题目】如图，△ABC三边的中线AD、BE、CF的公共点为G，若S△ABC=12，则图中阴影部分的面积是 ．

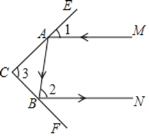
如图，一束光线MA照射到平面镜CE上，被CE反射到平面镜CF上，又被CF反射．已知被CF反射出的光线BN与光线MA平行．若∠1=35°，则∠2= ，∠3= ；若∠1=50°，∠3= ．

（2）由（1）猜想：当两平面镜CE，CF的夹角∠3为多少度时，可以使任何射到平面镜CE上的光线MA，经过平面镜CE，CF的两次反射后，入射光线MA与反射光线BN平行，请你写出推理过程．

【题目】如图，已知正△ABC的边长为2，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数图象大致是（ ）

A.
B.
C.
D.

【题目】如图，在平面直角坐标系中，正方形ABCO的对角线BO在x 轴上，若正方形ABCO的边长为，点B在x负半轴上，反比例函数的图象经过C点．

（1）求该反比例函数的解析式；

（2）当函数值＞-2时，请直接写出自变量x的取值范围；

（3）若点P是反比例函数上的一点，且△PBO的面积恰好等于正方形ABCO的面积，求点P的坐标．

【题目】如图，在平面直角坐标系中，菱形的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数的图象上，点D的坐标为．将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上．

如图，点E在AB上，点F在CD上，∠1＝∠2，∠B＝∠C，求证AB∥CD．

证明：∵∠1＝∠2（已知），∠1＝∠4（　 　），

∴∠2＝　 　（等量代换），

∴　 　∥BF（　 　），

∴∠3＝∠　 　（　 　）．

又∵∠B＝∠C（已知），

∴∠3＝∠B（　 　），

∴AB∥CD（　 　）．

解：设x－4＝a，x－9＝b，则(x－4)(x－9)＝ab＝6，a－b＝(x－4)－(x－9)＝5，

∴(x－4)2+(x－9)2＝a2+b2＝(a－b)2＋2ab＝52＋2×6＝37

请仿照上面的方法求解下面问题：

(1)若x满足(x－2)(x－5)＝10，求(x－2)2 + (x－5)2的值

(2)已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，且AE＝1，CF＝3，长方形EMFD的面积是15，分别以MF、DF作正方形，求阴影部分的面积．