（1）求证：AE＝CE；

（2）若BC＝，求AB的长．

【题目】我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．
（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；
（2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？

【题目】如图，广安市防洪指挥部发现渠江边一处长400米，高8米，背水坡的坡角为45°的防洪大堤（横截面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：背水坡面用土石进行加固，并使上底加宽2米，加固后，背水坡EF的坡比i=1：2．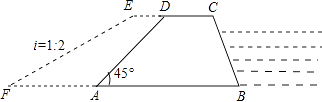

（1）求加固后坝底增加的宽度AF的长；
（2）求完成这项工程需要土石多少立方米？

【题目】如图，已知.求．以下是某位同学的解答过程，请在横线上填空，将解答过程补充完整．

解：分别过的平行线

∵ （辅助线）

∴（如果两条直线都与第三条直线平行，那么这两条直线平行）

∴

（　 　）

（　 　）

∵ （已知）

∴ （等式的性质）

∵（已证）

∴ （等式的性质）

∵（已知）

（已证）

∴ （等量代换）

如果两条平行线被三条直线所截，那么一对内错角的角平分线一定互相平行．

已知：AB∥CD，EM平分∠AEF，FN平分∠EFD

求证： EM∥FN

证明：

∵AB∥CD

∴∠AEF=∠DFE （ ）

∵EM平分∠AEF

∴∠MEF=∠ AEF （ ）

∵FN平分∠EFD

∴∠EFN=∠ EFD （ ）

∴∠MEF=∠ EFN

∴ EM ∥FN （ ）

【题目】如图，有A，B两个转盘，其中转盘A被分成4等份，转盘B被分成3等份，并在每一份内标上数字．现甲、乙两人同时各转动其中一个转盘，转盘停止后（当指针指在边界线上时视为无效，重转），若将A转盘指针指向的数字记为x，B转盘指针指向的数字记为y，从而确定点P的坐标为P（x，y）．

（1）请用列表或画树状图的方法写出所有可能得到的点P的坐标；
（2）计算点P在函数y= 图象上的概率．

【题目】如图，在平面直角坐标系中，已知的三个顶点的坐标分别为

（1）请按下列要求画图：

①将先向右平移个单位长度、再向上平移个单位长度，得到，画出

②与关于原点成中心对称，画出

③画出绕点顺时针旋转后得到的

（2）在中所得的和关于点成中心对称，请直接写出对称中心点的坐标．

【题目】如图，已知△ABC是等边三角形，点D，E分别在边BC，AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF，CF，连接BE并延长交CF于点G．下列结论：
①△ABE≌△ACF；②BC=DF；③S△ABC=S△ACF+S△DCF；④若BD=2DC，则GF=2EG．其中正确的结论是 ． （填写所有正确结论的序号）

（1）当DE∥BC时，△ACD的形状按角分类是直角三角形；

（2）在点D的运动过程中，△ECD的形状可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由．

（1）问符合题意的搭配方案有几种？请你帮助设计出来.

（2）若搭配一个A种造型的费用是800元，搭配一个B种造型的费用是960元，试说明（1）中哪种方案费用最低？最低费用是多少元？