【题目】如图①，在中，已知分别是上的两点，且．．

求梯形的面积；

如图②，有一梯形与梯形重合，固定，将梯形向右运动，当点D与点C重合时梯形停止运动；

①若某时段运动后形成的四边形中，求运动路程的长，并求此时的值；

②设运动中的长度为，试用含的代数式表示梯形与重合部分面积．

(1)洗衣机的进水时间是多少分钟？清洗时洗衣机中水量为多少升？

(2)已知洗衣机的排水速度为每分钟19升．

①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式；

②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量．

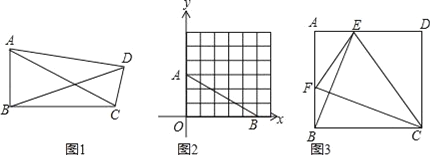
（1）①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=　 　；

②如图2，直角坐标系中，A（0，3），B（5，0），若整点P使得四边形AOBP是准矩形，则点P的坐标是　 　；（整点指横坐标、纵坐标都为整数的点）

（2）如图3，正方形ABCD中，点E、F分别是边AD、AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；

（3）已知，准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是　 　．

【题目】在正方形中，动点分别从两点同时出发，以相同的速度在直线上移动；

(1)如图①,当分别移动到边的延长线上时，连接和与的关系为____ ；

(2)如图②，己知正方形的边长为点和分别从点同时出发，以相同的速度沿方向向终点和运动，连接和，交于点，请你画出点运动路线的草图，试求出线段的最小值．

(3)如图③，在(2)的条件下，求周长的最大值；

【题目】如图， 圆柱形容器中，高为底面周长为在容器内壁离容器底部的点处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿与蚊子相对的点处，则壁虎捕捉蚊子的最短距离为___(容器厚度忽略不计． )

（1）根据上表信息，下列三个函数关系式中，刻画q，v关系最准确的是（只需填上正确答案的序号）① ② ③
（2）请利用（1）中选取的函数关系式分析，当该路段的车流速为多少时，流量达到最大？最大流量是多少？
（3）已知q，v，k满足 ，请结合（1）中选取的函数关系式继续解决下列问题：
①市交通运行监控平台显示，当 时道路出现轻度拥堵，试分析当车流密度k在什么范围时，该路段出现轻度拥堵；
②在理想状态下，假设前后两车车头之间的距离d（米）均相等，求流量q最大时d的值

【题目】如图，将线段AB绕点A逆时针旋转60°得AC，连接BC，作△ABC的外接圆⊙O，点P为劣弧 上的一个动点，弦AB，CP相交于点D．

（1）求∠APB的大小；
（2）当点P运动到何处时，PD⊥AB？并求此时CD：CP的值；
（3）在点P运动过程中，比较PC与AP+PB的大小关系，并对结论给予证明．

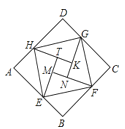
【题目】如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为,若，则的值是_______．

A. 5≤a≤12B. 12≤a≤3

C. 12≤a≤4D. 12≤a≤13

如图1，点是线段外一动点，且，．当点位于 时，线段的长取得最大值；最大值为 (用含，的式子表示)．

(2)应用：

如图2，点为线段外一动点，，，分别以，为边在外部作等边和等边，连接，．

①求证：；

②直接写出线段长的最大值．

(3)拓展：

如图3，在平面直角坐标系中，点，点，点为线段外一动点，，，，请直接写出线段长的最大值及此时点的坐标．