
科目: 来源: 题型:
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).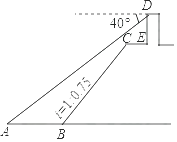
A.5.1米
B.6.3米
C.7.1米
D.9.2米
查看答案和解析>>
科目: 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.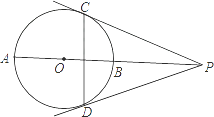
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO= ![]() ,求PO的长.
,求PO的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】开展“创卫”活动,某校倡议学生利用双休日在“人民公园”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
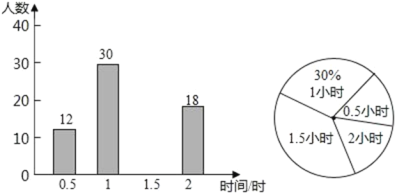
(1)将条形统计图补充完整;
(2)求抽查的学生劳动时间的众数、中位数;
(3)电视台要从参加义务劳动的学生中随机抽取1名同学采访,抽到时参加义务劳动的时间为2小时的同学概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且![]() +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿平行于x轴的负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标. 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=![]() x+2与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
x+2与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求A、B的坐标;
(2)求△ABO的面积;
(3)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式.
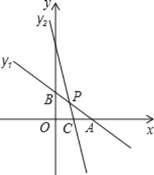
查看答案和解析>>
科目: 来源: 题型:
【题目】我们提供如下定理:在直角三角形中,30°的锐角所对的直角边是斜边的一半,
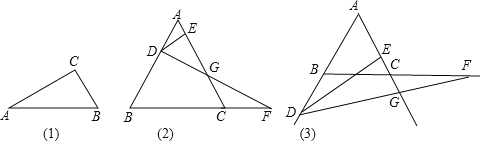
如图(1),Rt△ABC中,∠C=90°,∠A=30°,则BC=![]() AB.
AB.
请利用以上定理及有关知识,解决下列问题:
如图(2),边长为6的等边三角形ABC中,点D从A出发,沿射线AB方向有A向B运动点F同时从C出发,以相同的速度沿着射线BC方向运动,过点D作DE⊥AC,DF交射线AC于点G.
(1)当点D运动到AB的中点时,直接写出AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图3的情况时,EG的长始终等于AC的一半吗?若改变,说明理由;若不变,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位,再向下平移4个长度单位得到点C.
(1)用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;
(2)若t=1时,平移线段AB,使点A、B到坐标轴上的点![]() 、
、![]() 处,指出平移的方向和距离,并求出点
处,指出平移的方向和距离,并求出点![]() 、
、![]() 的坐标;
的坐标;
(3)若t=0时,平移线段AB至MN(点A与点M对应),使点M落在x轴的负半轴上,三角形MNB的面积为4,试求点M、N的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求: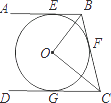
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】(背景知识)研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点![]() 、
、![]() ,则线段AB的中点坐标可以表示为
,则线段AB的中点坐标可以表示为![]()

(简单应用)如图1,直线AB与y轴交于点![]() ,与x轴交于点
,与x轴交于点![]() ,过原点O的直线L将
,过原点O的直线L将![]() 分成面积相等的两部分,请求出直线L的解析式;
分成面积相等的两部分,请求出直线L的解析式;
(探究升级)小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,![]() 试说明
试说明![]() ;
;
(综合运用)如图3,在平面直角坐标系中![]() ,
,![]() ,
,![]() ,若OC恰好平分四边形OACB的面积,求点C的坐标.
,若OC恰好平分四边形OACB的面积,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com