
科目: 来源: 题型:
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |

请你结合图表中所提供的信息,回答下列问题:
(1)表中m= ,n= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,![]() 这一组所占圆心角的度数为 度;
这一组所占圆心角的度数为 度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1 , 交x轴正半轴于点O2 , 以O2为圆心,O2O为半径画圆,交直线l于点P2 , 交x轴正半轴于点O3 , 以O3为圆心,O3O为半径画圆,交直线l于点P3 , 交x轴正半轴于点O4;…按此做法进行下去,其中 ![]() 的长为 .
的长为 . 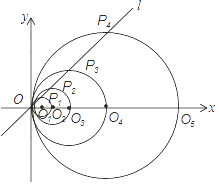
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下面证明:

(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b.
证明:∵a⊥c (已知)
∴∠1= (垂直定义)
∵b∥c (已知)
∴∠1=∠2 ( )
∴∠2=∠1=90° ( )
∴a⊥b ( )
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE.
证明:∵AB∥CD (已知)
∴∠B= ( )
∵∠B+∠D=180° (已知)
∴∠C+∠D=180° ( )
∴CB∥DE ( )
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
A.![]() π
π
B.![]() π
π
C.6π
D.![]() π
π
查看答案和解析>>
科目: 来源: 题型:
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数_____,2018应排在A,B,C,D,E中的_____位置.

查看答案和解析>>
科目: 来源: 题型:
【题目】五子棋深受广大棋友的喜爱,其规则是:在 15 15 的正方形棋盘中,由黑方先行,轮流奕子,在任何一方向(横向、竖向或斜线 方向)上连成五子者为胜。如图 3 是两个五子棋爱好者甲和乙的 部分对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若 A 点的位置记作(8,4),若不让乙在短时间内获胜,则甲必须落子 的位置是___________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )
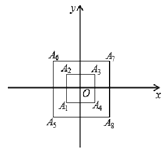
A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境:如图,已知AB∥CD,∠1=∠2,求证:∠3=∠4.

解法展示:证明:延长BE交直线CD于点M,如图所示.

∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是_____________,根据4是____________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com