
科目: 来源: 题型:
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


查看答案和解析>>
科目: 来源: 题型:
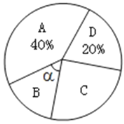
【题目】2019年10月,某市高质量通过全国文明城市测评,该成绩的取得得益于领导高度重视(A)、整改措施有效(B)、市民积极参与(C)、市民文明素质(D).某数学兴趣小组随机走访了部分市民,对这四项认可度进行调查(只选填最认可的一项),并将调查结果制作了如下两幅不完整的统计图.
(1)请补全D项的条形图;
(2)已知B、C两项条形图的高度之比为3:5.
①选B、C两项的人数各为多少个?
②求α的度数,

查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ 。
_________ 。
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值。
的值。
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式。
的形式。
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
科目: 来源: 题型:
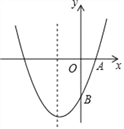
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.


请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:

(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知等腰△ABC顶角∠A=36°.
(1)尺规作图:在AC上作一点D,使AD=BD;(保留作图痕迹,不必写作法和证明)
(2)求证:△BCD是等腰三角形.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
如图1,![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

操作发现:如图2,保持点![]() 不动,
不动,![]() 绕点
绕点![]() 按顺时针旋转角度
按顺时针旋转角度![]() (
(![]() ),连接
),连接![]() 与
与![]() .
.

(1)猜想线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:如图3,![]() 绕点
绕点![]() 继续按顺时针旋转,当点
继续按顺时针旋转,当点![]() ,
,![]() ,
,![]() 在同一直线上时,过点
在同一直线上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(2)求![]() 的度数;
的度数;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的的数量关系.
之间的的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式
分解的方法,其中运用公式法即运用平方差公式:![]() 和完全平方公式:
和完全平方公式:![]() 进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式![]()
![]() 变形为
变形为![]() 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式![]() 的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:![]()
![]()

![]()
![]() .
.
根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将![]() 化成
化成![]() 的形式为_______;
的形式为_______;
(2)请你利用上述方法因式分解:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com