
科目: 来源: 题型:
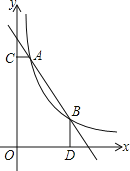
【题目】如图,一次函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 轴于C,
轴于C,![]() 轴于D
轴于D
![]() 求k的值;
求k的值;
![]() 根据图象直接写出
根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
![]() 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若![]() 和
和![]() 面积相等,求点P坐标.
面积相等,求点P坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)

查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
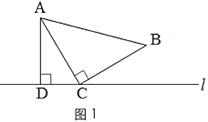
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
初步探究:
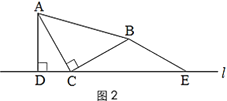
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
变式拓展:
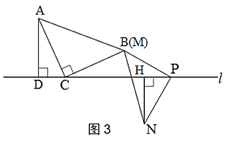
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
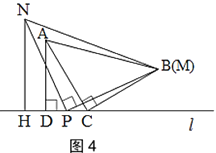
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某贸易公司购进“长青”胶州大白菜,进价为每棵20元,物价部门规定其销售单价每棵不得超过80元,也不得低于30元.经调查发现:日均销售量y(棵)与销售单价x(元/棵)满足一次函数关系,并且每棵售价60元时,日均销售90棵;每棵售价30元时,日均销售120棵.
(1)求日均销售量y与销售单价x的函数关系式;
(2)在销售过程中,每天还要支出其他费用200元,求销售利润w(元)与销售单价x之间的函数关系式;并求当销售单价为何值时,可获得最大的销售利润?最大销售利润是多少?
查看答案和解析>>
科目: 来源: 题型:
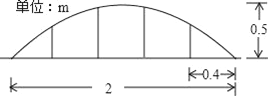
【题目】某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,完成相应的任务:
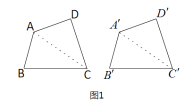
全等四边形根据全等图形的定义可知:四条边分别相等,四个角也分别相等的两个四边形全等.在“探索三角形全等的条件” 时,我们把两个三角形中“一条边相等” 或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法,探索“四边形全等的条件”,进行了如下思考:如图 1,四边形ABCD和四边形A'B'C'D'中,连接对角线AC,A'C',这样两个四边形全等的问题就转化为“△ABC≌△A'B'C'”与“△ACD ≌ △A 'C 'D '”的问题.若先给定“△ABC≌△A'B'C'”的条件,只要再增加2个条件使“△ACD≌△A'C'D'”即可推出两个四边形中“四条边分别相等,四个角也分别相等”,从而说明两个四边形全等.
按照智慧小组的思路,小明对图1中的四边形ABCD和四边形A'B'C'D'先给出如下条件:AB=A'B',∠B=∠B',BC=B'C',小亮在此基础上又给出“AD=A'D',CD=C'D'”两个条件,他们认为满足这五个条件能得到“四边形ABCD≌四边形A'B'C'D'”.
(1)请根据小明和小亮给出的条件,说明“四边形ABCD≌四边形A'B'C'D'”的理由;
(2)请从下面A,B两题中任选一题作答,我选择______题.
A.在材料中“小明所给条件”的基础上,小颖又给出两个条件“AD=A'D',∠BCD=∠B'C'D'”,满足这五个条件_______(填“能”或“不能”)得到“四边形 ABCD≌四边形A'B'C'D'”.
B.在材料中“小明所给条件”的基础上,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使“四边形ABCD≌四边形A'B'C'D'”,你添加的条件是:①___________;②__________.:
查看答案和解析>>
科目: 来源: 题型:
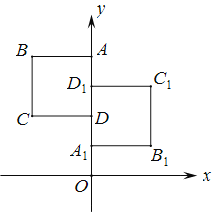
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系:

(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)在当地温度![]() 每增加
每增加![]() ,这种蟋蟀
,这种蟋蟀![]() 叫的次数
叫的次数![]() 是怎样变化的?
是怎样变化的?
(3)这种蟋蟀![]() 叫的次数
叫的次数![]() (次)与当地温度
(次)与当地温度![]() 之间的关系为 ;
之间的关系为 ;
(4)当这种蟋蟀![]() 叫的次数
叫的次数![]() 时,求当时该地的温度.
时,求当时该地的温度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com