【题目】如图所示， 是的角平分线，以点为圆心， 为半径作圆交的延长线于点，交于点，交于点，且．

（）求证： ；

（）求证：点是的中点；

（）如果，求半径的长．

【题目】如图，在平面直角坐标系xOy中，直线y=--x＋8与x轴，y轴分别交于点A，点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．

(1)求AB的长和点C的坐标；

(2)求直线CD的表达式．

【题目】某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数： ．

（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？

（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？

（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）

（1）若∠EOC=80°，求∠BOD的度数；

（2）若∠EOC=∠EOD，求∠BOD的度数．

请根据所提供的信息解答下列问题：

(1)频率统计表中a＝________，b＝_______；

(2)请补全频数分布直方图；

(3)请根据抽样统计结果，估计该次大赛中成绩不低于41分的学生有多少人？

(1)求证：△ACE≌△BCD；

(2)若AD＝5，BD＝12，求DE的长．

【题目】如图，在正方形中， 为对角线， 的交点，经过点和点作⊙，分别交， 于点， ．已知正方形边长为，⊙的半径为，则的值为__________．

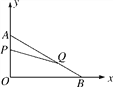
(1)求直线AB的解析式；

(2)当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？

(3)当t＝2秒时，四边形OPQB的面积为多少个平方单位？

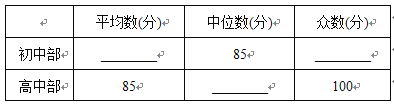
(1)根据图示填写下表；

(2)结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．

（1）求证：四边形AMDN是平行四边形；

（2）填空：①当AM的值为 时，四边形AMDN是矩形；②当AM的值为 时，四边形AMDN是菱形。