
科目: 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF。

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.

(1)若自由转动转盘,当它停止转动时,指针指向奇数区的概率是多少?
(2)若自由转动转盘,当它停止转动时,指针指向的数小于或等于4的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在平面直角坐标系中,A(0,﹣1)、B(﹣2,0)C(4,0)
(1)求△ABC的面积;
(2)在y轴上是否存在一个点D,使得△ABD为等腰三角形,若存在,求出点D坐标;若不存,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A(3,0),B(0,3),过点B画y轴的垂线l,点C在线段AB上,连结OC并延长交直线l于点D,过点C画CE⊥OC交直线l于点E.
(1)求∠OBA的度数,并直接写出直线AB的解析式;
(2)若点C的横坐标为2,求BE的长;
(3)当BE=1时,求点C的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
【答案】(1)m的值为6;(2)17.
【解析】试题分析:
(1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值;
(2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m的值(此时m的取值需满足根的判别式△![]() ),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
②当7为底边时,则方程的两根相等,由此可得“根的判别式△=0”,从而可得关于m的方程,解方程求得m的值,代入原方程可求得方程的两根,再由三角形三边之间的关系检验即可.
试题解析:
(1)(x1-1)(x2-1)=28,即x1x2-(x1+x2)=27,而x1+x2=2(m+1),x1x2=m2+5,
∴m2+5-2(m+1)=27,
解得m1=6,m2=-4,
又Δ=[-2(m+1)]2-4×1×(m2+5)≥0时,m≥2,
∴m的值为6;
(2) 若7为腰长,则方程x2-2(m+1)x+m2+5=0的一根为7,
即72-2×7×(m+1)+m2+5=0,
解得m1=10,m2=4,
当m=10时,方程x2-22x+105=0,根为x1=15,x2=7,不符合题意,舍去.
当m=4时,方程为x2-10x+21=0,根为x1=3,x2=7,此时周长为7+7+3=17
若7为底边,则方程x2-2(m+1)x+m2+5=0有两等根,
∴Δ=0,解得m=2,此时方程为x2-6x+9=0,根为x1=3,x2=3,3+3<7,不成立,
综上所述,三角形周长为17
点睛:(1)一元二次方程根与系数的关系成立的前提条件是方程要有实数根,即“根的判别式△![]() ”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
【题型】解答题
【结束】
21
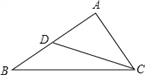
【题目】如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.
【答案】5![]() .
.
【解析】试题分析:
由点D是AB的中点,AB=10,易得AD=5;再由∠ACD=∠B,∠A=∠A,可证得:
△ACD∽△ABC,从而可得: ![]() ,由此得到:AC2=AD
,由此得到:AC2=AD![]() AB=50即可解得AC的值.
AB=50即可解得AC的值.
试题解析:
∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC.
∴![]() ,
,
∴AC2=AD![]() AB.
AB.
∵D是AB的中点,AB=10,
∴AD=![]() AB=5,
AB=5,
∴AC2=50.
解得AC=![]() .
.
【题型】解答题
【结束】
22
【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com