
科目: 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
(1)若AC =9cm,CB = 6 cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB =![]() cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
(3)若C在线段AB的延长线上,且满足AC![]() BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】两个反比例函数![]() ,
,![]() 在第一象限内的图象如图所示,点P1,P2,P3,…,P2011
在第一象限内的图象如图所示,点P1,P2,P3,…,P2011
在反比例函数![]() 图象上,它们的横坐标分别是x1,x2,x3,…,x2011,纵坐标分别是1,3,5,…,共2011个连续奇数,过点P1,P2,P3,…,P2011分别作y轴的平行线,与
图象上,它们的横坐标分别是x1,x2,x3,…,x2011,纵坐标分别是1,3,5,…,共2011个连续奇数,过点P1,P2,P3,…,P2011分别作y轴的平行线,与![]() 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2005(x2011,y2011),则y2011=________.
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2005(x2011,y2011),则y2011=________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系,请从你所得两个关系中选出任意一个,说明你探究的结论的正确性.

结论:(1)
(2)
选择结论: ,说明理由.
查看答案和解析>>
科目: 来源: 题型:
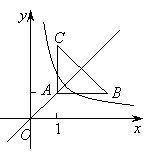
【题目】如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线![]() (k≠0)与
(k≠0)与![]() 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )

A. (0,-2) B. (-1,-1) C. (-1,0) D. (1,-2)
查看答案和解析>>
科目: 来源: 题型:
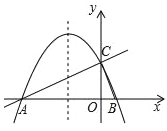
【题目】在如图所示的平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,与x轴的另一交点为点B,其对称轴是
与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,与x轴的另一交点为点B,其对称轴是![]() .
.
(1)求抛物线解析式.
(2)抛物线上是否存在点M(点m不与点C重合),使△MAB与△ABC的面积相等?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
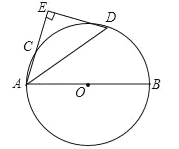
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果∠BAC=60°,AD=4,求AC长.
查看答案和解析>>
科目: 来源: 题型:
【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这种图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?请解决以下问题:
(1)观察“规形图”,试探究∠BPC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图2:已知△ABC,BP平分∠ABC,CP平分∠ACB,直接写出∠BPC与∠A之间存在的等量关系为: .
迁移运用:如图3:在△ABC中,∠A=80°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠OPC=100°,则∠ACB的度数 .
②如图4:若D点是△ABC内任意一点,BP平分∠ABD,CP平分∠ACD.直接写出∠BDC、∠BPC、∠A之间存在的等量关系为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com