
科目: 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

(探究展示)
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
(拓展延伸)
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
科目: 来源: 题型:
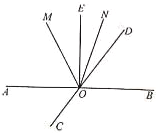
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD中,E、F分别是边AD,BC的中点.张老师请同学们将纸条的下半部分即平行四边形ABFE沿EF翻折,得到一个V字形图案.
(1)请你在原图中画出翻折后的图形平行四边形A′B′FE(用尺规作图,不写画法,保留作图痕迹)
(2)已知∠A=63°,求∠B′FC的大小.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
在进行二次根式的化简与运算时,我们有时会碰上如![]() 样的式子,其实我们还可以将其进一步化简:
样的式子,其实我们还可以将其进一步化简:
(1)![]() ···(一)
···(一)
(2)![]() ···(二)
···(二)
(3) ···(三)
···(三)
以上这种化简的步骤叫做分母有理化.
![]() 还可以用以下方法化简:
还可以用以下方法化简: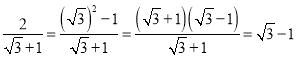 ···(四)
···(四)
请完成下列问题:
(1)请计算![]() ;
;
(2)当![]() ,则代数式
,则代数式![]() 的值为 ;
的值为 ;
(3)请参照(三)式和(四)式用两种不同的方法化简![]()
(4)化简:![]()
查看答案和解析>>
科目: 来源: 题型:
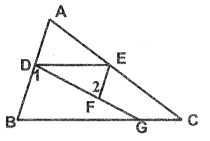
【题目】已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180°( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180°( )
所以 ∥ ( )
所以∠1=∠2( )
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四个函数:
①y=kx(k为常数,k>0)
②y=kx+b(k,b为常数,k>0)
③y=![]() (k为常数,k>0,x>0)
(k为常数,k>0,x>0)
④y=ax2(a为常数,a>0)
其中,函数y的值随着x值得增大而减少的是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目: 来源: 题型:
【题目】画图,并完成填空:
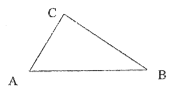
已知直角三角形ABC,∠C=90°
(1)过点B作直线1平行于AC
(2)利用尺规,画出线段AC的垂直平分线EF,交AB于点E,AC于点F
(3)点A到点E的距离是线段 的长,点A到BC的距离是线段 的长,直线L与AC的距离是线段 的长
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是长方形纸带,将纸带沿折叠成图2,再沿即折叠成图3,若在图1中∠DEF=a,则图3中∠CFE用含有a的式子表示=_______(0<a<60°) .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com