
科目: 来源: 题型:
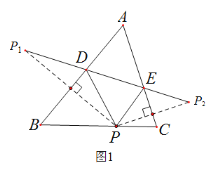
【题目】(1)如图1,在△ABC中,∠A![]() ,P是BC边上的一点,
,P是BC边上的一点,![]() ,
,![]() 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结![]() ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E.
①若![]() ,求
,求![]() 的度数;
的度数;
②请直接写出∠A与![]() 的数量关系:___________________________;
的数量关系:___________________________;
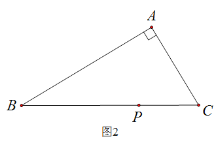
(2)如图2,在△ABC中,若∠BAC![]() ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点![]() 、
、![]() ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点![]() ,
,![]() 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某县政府部门决定,招标一工程队负责完成一座水库的土方施工任务.该工程队有A,B两种型号的挖掘机,已知1台A型和2台B型挖掘机同时施工1小时共挖土80立方米,2台A型和3台B型挖掘机同时施工1小时共挖土140立方米.每台A型挖掘机一个小时的施工费用是350元,每台B型挖掘机一个小时的施工费用是200元.
(1)分别求每台A型,B型挖掘机一小时各挖土多少立方米?
(2)若A型和B型挖掘机共10台同时施工4小时,至少完成1360立方米的挖土量,且总费用不超过14000元.问施工时有哪几种调配方案?且指出哪种调配方案的施工费用最低,最低费用多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E为AD边上的一点,过C点作CF⊥CE交AB的延长线于点F.
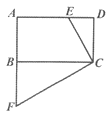
(1)求证:△CDE∽△CBF;
(2)若B为AF的中点,CB=3,DE=1,求CD的长.
查看答案和解析>>
科目: 来源: 题型:
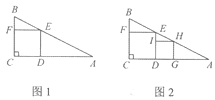
【题目】我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
(1)如图l,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是________;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推,则第n个内接正方形的边长an=____. (n为正整数)
查看答案和解析>>
科目: 来源: 题型:
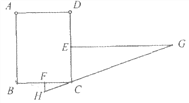
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长9里,城墙BC长7里,东门所在的点E,南门所在的点F分别是CD,BC的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=________里.
查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题(1)、(2)、(3).
例:解绝对值方程:![]() .
.
解:讨论:①当![]() ≥0时,原方程可化为
≥0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
②当![]() <0时,原方程可化为
<0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
∴原方程的解为![]() 和
和![]() .
.
问题(1):依例题的解法,方程![]() 的解是 ;
的解是 ;
问题(2):尝试解绝对值方程:![]() ;
;
问题(3):在理解绝对值方程解法的基础上,解方程:
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.

(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知△ABC的顶点均为网格线的交点.
(1)将△ABC向下平移5个单位长度,再向左平移1个单位长度,画出平移后的△A1B1C1;
(2)画出△A1B1C1关于直线l轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C3以A、A3、B、B3为顶点的四边形的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com