
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)求线段![]() 的长度;
的长度;
(2)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤![]() .当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .
.当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .

查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】某保温杯专卖店通过市场调研,准备销售![]() 、
、![]() 两种型号的保温杯,其中每件
两种型号的保温杯,其中每件![]() 种保温杯的进价比
种保温杯的进价比![]() 种保温杯的进价高20元,已知专卖店用3200元购进
种保温杯的进价高20元,已知专卖店用3200元购进![]() 种保温杯的数量与用2560元购进
种保温杯的数量与用2560元购进![]() 种保温杯的数量相同.
种保温杯的数量相同.
(1)求两种保温杯的进价;
(2)若![]() 种保温杯的售价为250元,
种保温杯的售价为250元,![]() 种保温杯的售价为180元,专卖店共进两种保温杯200个,设
种保温杯的售价为180元,专卖店共进两种保温杯200个,设![]() 种保温杯进货
种保温杯进货![]() 个,求该专卖店获得的总利润
个,求该专卖店获得的总利润![]() (元)与
(元)与![]() 种保温杯进货数
种保温杯进货数![]() (个)之间的函数关系式,并写出自变量的取值范围.
(个)之间的函数关系式,并写出自变量的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲,乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,根据图象信息回答下列问题:
(分钟)之间的函数关系如图所示,根据图象信息回答下列问题:

(1)图书馆与学校之间的距离为 米;
(2)当![]() 分钟时,甲乙两人相遇;
分钟时,甲乙两人相遇;
(3)乙的速度为 米/分钟;
(4)![]() 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.
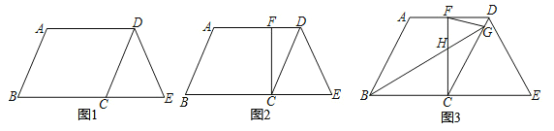
(1)如图1,求证:CD=DE;
(2)如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系_______________________;
(3)如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 两地相距
两地相距![]() ,甲、乙两人沿同一公路从
,甲、乙两人沿同一公路从![]() 地出发到
地出发到![]() 地,甲骑摩托车,乙骑自行车,如图中
地,甲骑摩托车,乙骑自行车,如图中![]() 分别表示甲、乙离开
分别表示甲、乙离开![]() 地的距离
地的距离![]() 与时间
与时间![]() 的函数关系的图象,结合图象解答下列问题.
的函数关系的图象,结合图象解答下列问题.
(1)甲比乙晚出发___小时,乙的速度是___![]() ;甲的速度是___
;甲的速度是___![]() .
.
(2)若甲到达![]() 地后,原地休息0.5小时,从
地后,原地休息0.5小时,从![]() 地以原来的速度和路线返回
地以原来的速度和路线返回![]() 地,求甲、乙两人第二次相遇时距离
地,求甲、乙两人第二次相遇时距离![]() 地多少千米?并画出函数关系的图象.
地多少千米?并画出函数关系的图象.

查看答案和解析>>
科目: 来源: 题型:
【题目】某瓜果基地市场部为指导该基地某种蔬菜的生产销售,在对历年市场行情和生产情况进行调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图所示.注:两图中的每个实心点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图象是线段,图乙的图象是抛物线.
请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?说明理由;
(3)已知市场部销售该种蔬菜,4、5两个月的总收益为48万元,且5月份的销量比4月份的销量多2万公斤,求4、5两个月销量各多少万公斤?

查看答案和解析>>
科目: 来源: 题型:
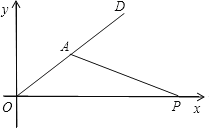
【题目】随着科学技术的发展,机器人早已能按照设计的指令完成各种动作.在坐标平面上,根据指令[S,α](S≥0,0°<α<180°)机器人能完成下列动作:先原地顺时针旋转角度α,再朝其对面方向沿直线行走距离s.
(1)填空:如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是 ;
(2)机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能截住小球.
(参考数据:sin53°≈0.8,cos37°≈0.80,tan37°≈0.75,tan26.5°≈0.5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com