
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,边AB、OA(AB>OA)的长分别是方程x2﹣11x+24=0的两个根,D是AB上的点,且满足![]() .
.
(1)矩形OABC的面积是 ,周长是 .
(2)求直线OD的解析式;
(3)点P是射线OD上的一个动点,当△PAD是等腰三角形时,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°.
(1)求证:EF=BE+DF;
(2)若线段EF、AB的长分别是方程x2﹣5x+6=0的两个根,求△AEF的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】今年5月,某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:

(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
查看答案和解析>>
科目: 来源: 题型:
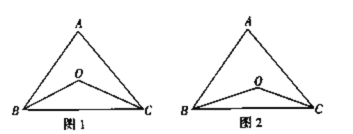
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的运货情况如下表:
(1)分别求甲、乙两种货车每辆载重多少吨?
(2)现租用该公司3辆甲种货车和5辆乙种货车刚好一次运完这批货物,如果按每吨付运费120元计算,货主应付运费多少元?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
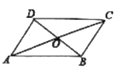
(1)求证:四边形ABCD是平行四边形
(2)若AC⊥BD,且AB=4,则四边形ABCD的周长为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人分别在六次射击中的成绩如下表:(单位:环)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
甲 | 6 | 7 | 7 | 8 | 6 | 8 |
乙 | 5 | 9 | 6 | 8 | 5 | 9 |
分别算出两人射击的平均数和方差.这六次射击中成绩发挥比较稳定的是谁?
查看答案和解析>>
科目: 来源: 题型:
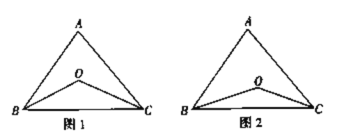
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,BC=a.作BC边的三等分点C1,使得CC1:BC1=1:2,过点C1作AC的平行线交AB于点A1,过点A1作BC的平行线交AC于点D1,作BC1边的三等分点C2,使得C1C2:BC2=1:2,过点C2作AC的平行线交AB于点A2,过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com