
科目: 来源: 题型:
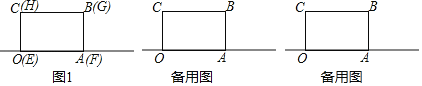
【题目】有两个大小完全一样的长方形OABC和EFGH重合放在一起,边OA、EF在数轴上,O为数轴原点(如图1),长方形OABC的边长OA的长为6个坐标单位.
(1)数轴上点A表示的数为 .
(2)将长方形EFGH沿数轴所在直线水平移动
①若移动后的长方形EFGH与长方形OABC重叠部分的面积恰好等于长方形OABC面积的![]() ,则移动后点F在数轴上表示的数为 .
,则移动后点F在数轴上表示的数为 .
②若出行EFGH向左水平移动后,D为线段AF的中点,求当长方形EFGH移动距离x为何值时,D、E两点在数轴上表示的数是互为相反数?
查看答案和解析>>
科目: 来源: 题型:
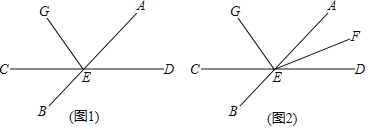
【题目】如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC= °;
(2)在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG=m°(m>90°)(如图2),则∠AEG﹣∠CEG= °(用m的代表式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校组织部分师生从学校(A地)到300千米外的B地进行红色之旅(革命传统教育),租用了客运公司甲、乙两辆车,其中乙车速度是甲车速度的![]() ,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.
,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.
(1)求甲、乙两车的速度?
(2)问甲车在C地结束休息后再行驶多长时间,甲、乙两车相距30千米?
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠A![]() 90°,AB
90°,AB![]() AC.
AC.
(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“![]() ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);
(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB![]()
![]() PA.
PA.
①如图2,点P在△ABC内,∠ABP![]() 30°,求∠PAB的大小;
30°,求∠PAB的大小;
②如图3,点P在△ABC外,连接PC,设∠APC![]() α,∠BPC
α,∠BPC![]() β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】对于⊙C与⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q可以与点P重合),且![]() ,则点P称为点A关于⊙C的“生长点”.
,则点P称为点A关于⊙C的“生长点”.
已知点O为坐标原点,⊙O的半径为1,点A(-1,0).
(1)若点P是点A关于⊙O的“生长点”,且点P在x轴上,请写出一个符合条件的点P的坐标________;
(2)若点B是点A关于⊙O的“生长点”,且满足![]() ,求点B的纵坐标t的取值范围;
,求点B的纵坐标t的取值范围;
(3)直线![]() 与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
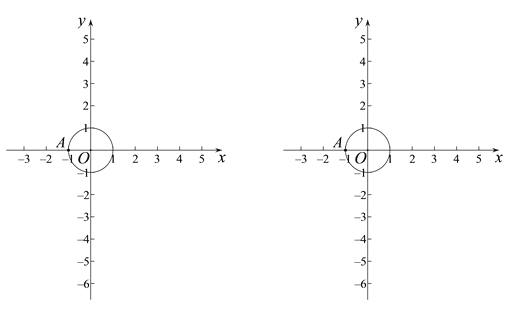
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.

(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图在平面直角坐标系xOy中,函数y1=![]() (x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是6,请写出点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.

小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com