
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资![]() (吨)与时间
(吨)与时间![]() (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
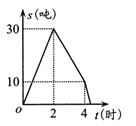
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在![]() 中,点
中,点![]() 在
在![]() 的平分线上,且
的平分线上,且![]() .
.

(1)如图1,若点![]() 在
在![]() 上,求证:
上,求证:![]() .
.
(2)如图2,若点![]() 在
在![]() 内部,求证:
内部,求证:![]() .
.
(3)猜想,若![]() 点在
点在![]() 的外部,
的外部,![]() 成立吗?请画图表示,不需要证明.
成立吗?请画图表示,不需要证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】某自行车厂计划每天生产![]() 辆自行车,但由于各种原因,实际每天生产量与计划生产量相比有所差异,下表是该厂某一周的实际生产情况(以计划产量为标准,超产记为正数,不足记为负数.单位:辆):
辆自行车,但由于各种原因,实际每天生产量与计划生产量相比有所差异,下表是该厂某一周的实际生产情况(以计划产量为标准,超产记为正数,不足记为负数.单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与标准产量的差 |
|
|
|
|
|
|
|
(![]() )根据表格,这一周该厂实际生产自行车多少辆?
)根据表格,这一周该厂实际生产自行车多少辆?
(![]() )若该厂实行“每日计件工资制”,每生产一辆自行车可得
)若该厂实行“每日计件工资制”,每生产一辆自行车可得![]() 元,若超额完成任务,则超出部分每辆额外奖励
元,若超额完成任务,则超出部分每辆额外奖励![]() 元;若未完成任务,则每少生产一辆扣
元;若未完成任务,则每少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少元?
元,那么该厂工人这一周的工资总额是多少元?
(![]() )若将(
)若将(![]() )中的“每日计件工资制”改为“每周计件工资制”,其他条件不变,在此方式下该厂工人一周的工资总额与“每日计件工资制”相比是减少还是增加了?减少或增加了多少?
)中的“每日计件工资制”改为“每周计件工资制”,其他条件不变,在此方式下该厂工人一周的工资总额与“每日计件工资制”相比是减少还是增加了?减少或增加了多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】现有一块长方形花园(如图一所示),长为![]() 米,宽为
米,宽为![]() 米,现准备在花园中间修建横竖两条小路(图中空白部分),已知横向小路的宽是竖向小路的宽的
米,现准备在花园中间修建横竖两条小路(图中空白部分),已知横向小路的宽是竖向小路的宽的![]() 倍,设竖向小路的宽为
倍,设竖向小路的宽为![]() 米(
米(![]() 为正数).
为正数).
(![]() )两条小路的面积之和是多少?
)两条小路的面积之和是多少?
(![]() )当
)当![]() 时,求花园剩余部分(阴影部分)的面积;
时,求花园剩余部分(阴影部分)的面积;
(3)若把竖向小路的宽改为原来的![]() 倍、横向小路的宽改为原来的一半(如图二所示),设图一与图二中花园剩余部分的面积分别为
倍、横向小路的宽改为原来的一半(如图二所示),设图一与图二中花园剩余部分的面积分别为![]() 、
、![]() ,求
,求![]() 与
与![]() 的差.
的差.

查看答案和解析>>
科目: 来源: 题型:
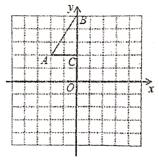
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度.![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() .
.
(1)将![]() 以点
以点![]() 为旋转中心旋转
为旋转中心旋转![]() ,得到
,得到![]() ,请画出
,请画出![]() 的图形.
的图形.
(2)将![]() 以
以![]() 为旋转中心,逆时针旋转
为旋转中心,逆时针旋转![]() ,得到
,得到![]() ,请画出
,请画出![]() 的图形.
的图形.
(3)线段![]() 的长度为______.
的长度为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点.
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com