
科目: 来源: 题型:
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,
,![]() 、
、![]() 分别是对角线
分别是对角线![]() ,
,![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上移动时,线段
上移动时,线段![]() 的最小值为________.
的最小值为________.

查看答案和解析>>
科目: 来源: 题型:
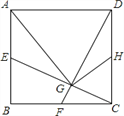
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=![]() AD.其中正确的有( )
AD.其中正确的有( )
A. ① ② B. ① ② ④ C. ① ③ ④ D. ① ② ③ ④
查看答案和解析>>
科目: 来源: 题型:
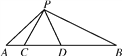
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE=________,EF=__________
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.(![]() 相遇时除外)
相遇时除外)
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.

查看答案和解析>>
科目: 来源: 题型:
【题目】为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量 ![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 成正比例;燃烧后,
成正比例;燃烧后,![]() 与
与![]() 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物![]() 分钟燃完,此时教室内每立方米空气含药量为
分钟燃完,此时教室内每立方米空气含药量为![]() .根据以上信息解答下列问题:
.根据以上信息解答下列问题:

(1)分别求出药物燃烧时及燃烧后 ![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当每立方米空气中的含药量低于![]() 时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于![]() 的持续时间超过
的持续时间超过![]() 分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
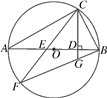
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,其中
两点,其中![]() 点坐标为
点坐标为![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
(3)一次函数的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数图象上的一个动点,若
是反比例函数图象上的一个动点,若![]() ,求此时
,求此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目: 来源: 题型:
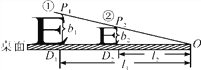
【题目】如图所示,在水平桌面上的两个“E”,当点P1,P2,O在一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力相同.
(1)图中b1,b2,l1,l2满足怎样的关系式?
(2)若b1=3.2 cm,b2=2 cm,①号“E”的测量距离l1=8 cm,要使测得的视力相同,则②号“E”的测量距离l2应为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com