
科目: 来源: 题型:
【题目】下列说法:(1)相反数是本身的数是正数;(2)两数相减,差小于被减数;(3)绝对值等于它相反数的数是负数;(4)倒数是它本身的数是1;(5)若![]() ,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目: 来源: 题型:
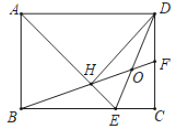
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①△ABE≌△ADH;②HE=CE;③H是BF的中点;④AB=HF;其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为90.
![]()
(1)请写出与A,B两点距离相等的M点对应的数;
(2)现在有一只电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,求C点对应的数是多少.
(3)若当电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,求经过多长的时间两只电子蚂蚁在数轴上相距35个单位长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目: 来源: 题型:
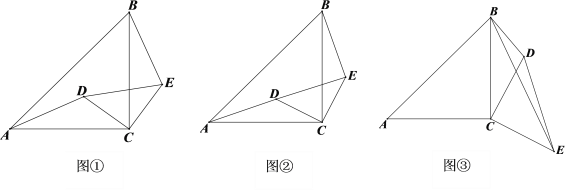
【题目】如图①已知△ACB和△DCE为等腰直角三角形,按如图的位置摆放,直角顶点
C重合.
(1)求证:AD=BE;
(2)将△DCE绕点C旋转得到图②,点A、D、E在同一直线上时,若CD=![]() ,BE=3,
,BE=3,
求AB 的长;
(3)将△DCE绕点C顺时针旋转得到图③,若∠CBD=45°,AC=6,BD=3,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】你能很快算出![]() 吗?
吗?
为了解决这个问题,我们考察个位上的数为5的正整数的平方,任意一个个位数为5的正整数可写成10n+5(n为正整数),即求![]() 的值,试分析
的值,试分析![]() ,2,3……这些简单情形,从中探索其规律.
,2,3……这些简单情形,从中探索其规律.
⑴通过计算,探索规律:
![]() 可写成
可写成![]() ;
;
![]() 可写成
可写成![]() ;
;
![]() 可写成
可写成![]() ;
;
![]() 可写成
可写成![]() ;………………
;………………
![]() 可写成________________________________
可写成________________________________
![]() 可写成________________________________
可写成________________________________
⑵根据以上规律,试计算![]() =
=
![]() =
=
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别为边AD,BC上的点,AE=CF,对角线AC平分∠ECF.
(1)求证:四边形AECF为菱形.
(2)已知AB=4,BC=8,求菱形AECF的面积.

查看答案和解析>>
科目: 来源: 题型:
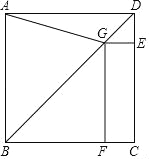
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭![]() 出发,晚上停留在
出发,晚上停留在![]() 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
+5,-8,+10,-12,+6,-18,+5,-2.
(1)![]() 处在岗亭
处在岗亭![]() 的什么方向?距离岗亭
的什么方向?距离岗亭![]() 多远?
多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
1637 年笛卡儿(R.Descartes,1596 1650)在其《几何学》中,首次应用待定系数法将 4 次方程分解为两个 2 次方程求解,并最早给出因式分解定理.
他认为,若一个高于二次的关于 x 的多项式能被 (![]() ) 整除,则其一定可以分解为 (
) 整除,则其一定可以分解为 (![]() ) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
例如:多项式![]() 可以分解为 (
可以分解为 (![]() ) 与另外一个整式 M 的乘积,即
) 与另外一个整式 M 的乘积,即 ![]()
令![]() 时,可知 x =1 为该方程的一个根.
时,可知 x =1 为该方程的一个根.
关于笛卡尔的“待定系数法”原理,举例说明如下: 分解因式:![]()
观察知,显然 x=1 时,原式 = 0 ,因此原式可分解为 (![]() ) 与另一个整式的积.
) 与另一个整式的积.
令:![]() ,则
,则![]() =
=![]() ,因等式两边 x 同次幂的系数相等,则有:
,因等式两边 x 同次幂的系数相等,则有: ,得
,得![]() ,从而
,从而![]()
此时,不难发现 x= 1 是方程 ![]() 的一个根.
的一个根.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)若![]() 是多项式
是多项式![]() 的因式,求 a 的值并将多项式
的因式,求 a 的值并将多项式![]() 分解因式;
分解因式;
(2)若多项式![]() 含有因式
含有因式![]() 及
及![]() ,求a+ b 的值.
,求a+ b 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com