
科目: 来源: 题型:
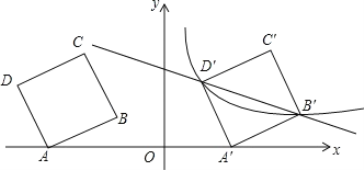
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(-6,0),D(-7,3),点B、C在第二象限内.
(1)点B的坐标 ;
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请求出符合题意的点P、Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形纸片ABCD中,AB=6,BC=8.
(1)将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,求BF的长;
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离.而|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离.类似的,有:|5﹣3|表示5、3在数轴上对应的两点之间的距离;|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
请根据绝对值的意义并结合数轴解答下列问题:
(1)画一条数轴。并在数轴上分别用A、B表示出1和3的两点
(2)数轴上表示1和3的两点之间的距离是 ;
(3)点A、B、C在数轴上分别表示有理数1、3、x,那么C到A的距离与C到B的距离之和可表示为 (用含绝对值的式子表示)
(4)若将数轴折叠,使得表示1和3的两点重合,则原点与表示数 的点重合
查看答案和解析>>
科目: 来源: 题型:
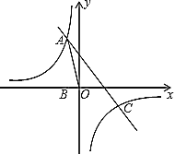
【题目】如图,反比例函数![]() 的图像经过第二象限内的点
的图像经过第二象限内的点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的面积为2.若直线
的面积为2.若直线![]() 经过点
经过点![]() ,并且经过反比例函数
,并且经过反比例函数![]() 的图像上另一点
的图像上另一点![]() .
.
(1)求反比例函数![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)不等式![]() 的解集为_________
的解集为_________
(4)若![]() 在
在![]()
![]() 图像上,且满足
图像上,且满足![]() ,则
,则![]() 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】把下面的有理数填在相应的大括号里:(★友情提示:将各数用逗号分开)
15,-![]() , 0,-0.15, -128,
, 0,-0.15, -128, ![]() ,+20,-2.6
,+20,-2.6
正数集合 { . . . ﹜;
负数集合 ﹛ . . . ﹜;
整数集合 ﹛ . . . ﹜;
非负数集合 ﹛ . . . ﹜.
查看答案和解析>>
科目: 来源: 题型:
【题目】我校对本校的八年级学生对待学习的态度进行了一次抽样调查,结果分成“非常感兴趣”、“比较感兴趣”、“一般般”、“不感兴趣”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.


根据所给数据,解答下列问题:
(1)本次问卷共随机调查了_________名学生,扇形统计图中![]() _________,扇形
_________,扇形![]() 所对应的圆心角为_________°;
所对应的圆心角为_________°;
(2)请根据数据信息补全条形统计图;
(3)若该校有2000名学生,估计选择“非常感兴趣”、“比较感兴趣”共约有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
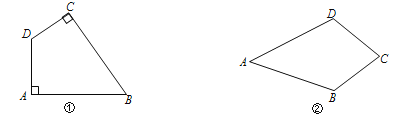
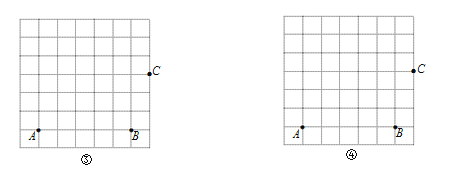
(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);
(2)下列说法正确的有 ;(填写所有正确结论的序号)
①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
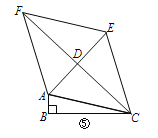
(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.
①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=![]() ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下面的几个算式:
1+2+1=4=2×2;1+2+3+2+1=9=3×3;
1+2+3+4+3+2+1=16=4×4;![]() 。
。
根据上面几道题的规律,计算下面的题:
1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1的值为__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com