
科目: 来源: 题型:
【题目】如图1,点A、D是抛物线![]() 上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).
上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).
(1) 若矩形ABCD的周长为3.5,求a的值;
(2) 求证:不论点A如何运动,∠EAD=∠ABE;
(3) 若△ABE是等腰三角形,
①求点A的坐标;
②如图2,若将直线BA绕点B按逆时针方向旋转至直线l,设点A、C到直线l的距离分别为![]() 、
、![]() ,求
,求![]() 的最大值.
的最大值.
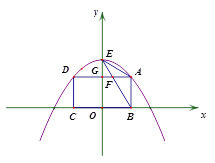
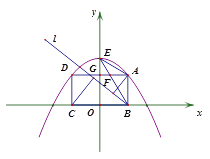
图1 图2
查看答案和解析>>
科目: 来源: 题型:
【题目】作图与计算:
在如图所示的正方形网格中,每个小正方形的边长为![]() ,格点三角形(顶点是网格线的交点的三角形)
,格点三角形(顶点是网格线的交点的三角形)![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.

(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)直接写出![]() 的面积及点
的面积及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东![]() 方向以每小时15海里的速度航行,甲沿南偏西
方向以每小时15海里的速度航行,甲沿南偏西![]() 方向以每小时
方向以每小时![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东![]() 方向追赶乙船,正好在B处追上
方向追赶乙船,正好在B处追上![]() 甲船追赶乙船的速度为多少海里
甲船追赶乙船的速度为多少海里![]() 小时?
小时?
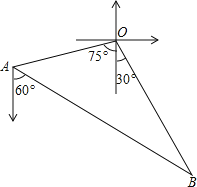
查看答案和解析>>
科目: 来源: 题型:
【题目】化简求值:
(1)当a=﹣1,b=2时,求代数式﹣2(ab﹣3b2)﹣[6b2﹣(ab﹣a2)]的值
(2)先化简,再求值:4xy﹣2(![]() x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
(3)若(2mx2﹣x+3)﹣(3x2﹣x﹣4)的结果与x的取值无关,求m的值
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
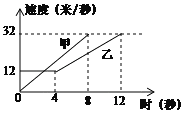
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABC内接于⊙O,AC是直径,点D是AC延长线上一点,且∠DBC=∠BAC, ![]() .
.
(1) 求证:BD是⊙O的切线;
(2) 求![]() 的值;
的值;
(3) 如图2,过点B作BG⊥AC交AC于点F,交⊙O于点G,BC、AG的延长线交于点E,⊙O的半径为6,求BE的长.
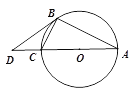
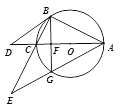
图1 图2
查看答案和解析>>
科目: 来源: 题型:
【题目】有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是 ;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.

查看答案和解析>>
科目: 来源: 题型:
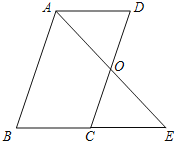
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com