A. 3B. 6C. D.

（1）求证：四边形BEDF是矩形；

（2）如图2，若M、N分别为AD、BC的中点，连接EM、EN、FM、FN，求证：四边形EMFN是平行四边形．

（1）游戏规则1：两人各摸1个球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由．

（2）游戏规则2； 两人同时各摸1个球，若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏小明赢得电影票的概率为　 　．

A. 两个转盘转出蓝色的概率一样大

B. 如果A转盘转出了蓝色，那么B转盘转出蓝色的可能性变小了

C. 先转动A 转盘再转动B 转盘和同时转动两个转盘，游戏者配成紫色的概率不同

D. 游戏者配成紫色的概率为

(1)是否存在实数k，使(2x1－x2)(x1－2x2)＝－成立？若存在，求出k的值；若不存在，请说明理由；

(2)求使－2的值为整数的整数k的值．

【题目】如图1，已知抛物线与x轴交于A,B两点，与y轴交于点C，顶点为D，点C’是点C关于对称轴的对称点，过点D作DG⊥x轴交x轴于点G，交线段AC于点E。

（1）连接DC，求△DCE的周长；

（2）如图2，点P是线段AC上方抛物线上的一点，过P作PH⊥x 轴交x轴于点H，交线段AC于点Q，当四边形PCQC’的面积最大时，在线段PH上有一动点M，在线段DG上有一动点N，在y轴上有一动点E，且满足MN⊥PH，连接AM,MN,NE,DE，求AM+MN+NE+DE的最小值；

（3）如图3，将抛物线沿直线AC进行平移，平移过程中的点D记为D’，点C记为C’，连接D’C’所形成的直线与x轴相交于点G，请问是否存在这样的点G，使得△D’OG为等腰三角形？若存在，求出此时OG的长度，若不存在，请说明理由。

图1 图2

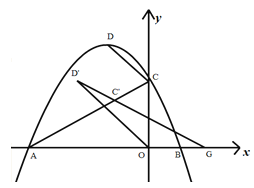
图3

A.5B.6C.4D.3

【题目】对任意一个三位数，如果满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为.例如，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，666÷111=6，所以.

（1）计算：和；

（2）若是“相异数”，证明：等于的各数位上的数字之和.

【题目】定义：任意两个数a,b,按规则c=a+b得到一个新数c，称所得的新数c为数a，b的“传承数。”

(1)若a=1，b=2，求a，b的“传承数”c；

(2)若a=1,b=,且+3x+1=0，求a，b的“传承数”c；

(3)若a=2n+1，b=n1，且a，b的“传承数”c值为一个整数，则整数n的值是多少?