
科目: 来源: 题型:
【题目】有依次排列的3个数:6,2,8,先将任意相邻的两个数,都用右边减去左边的数,所得之差写在这两个数之间,可产生一个新的数串:6,-4,2,6,8这称为第一次操作;做第二次同样操作后也可产生一个新数串:6,-10,-4,6,2,4,6,2,8,继续依次操作下去,问:从数串中6,2,8开始操作第2019次后所产生的那个新数串的所有数之和是( )
A.4054B.4056C.4058D.4060
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,![]() 为正方形
为正方形![]() 的边
的边![]() 上一点,将正方形
上一点,将正方形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,连接并延长
处,连接并延长![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,求证:
,求证:![]()
(3)如图3,点![]() 分别在
分别在![]() 边上,点
边上,点![]() 分别在
分别在![]() 边上,
边上,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:对于排好顺序的三个数:![]() 称为数列
称为数列![]() .将这个数列如下式进行计算:
.将这个数列如下式进行计算: ![]() ,
,![]() ,
,![]() ,所得的三个新数中,最大的那个数称为数列
,所得的三个新数中,最大的那个数称为数列![]() 的“关联数值”.
的“关联数值”.
例如:对于数列![]() 因为
因为![]()
![]()
![]() 所以数列
所以数列![]() 的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列
的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列![]() 的 “关联数值”为0;数列
的 “关联数值”为0;数列![]() 的“关联数值”为3...而对于“
的“关联数值”为3...而对于“![]() ”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.
”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.
(1)数列![]() 的“关联数值”为_______;
的“关联数值”为_______;
(2)将“![]() ”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______
”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______
(3)将“![]() ”
”![]() 这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求
这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求![]() 的值,并写出取得“关联数值”最大值的数列.
的值,并写出取得“关联数值”最大值的数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 和
和![]() 有一条公共边
有一条公共边![]() ,且
,且![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
(1)画出图形;
(2)若![]() ,
,![]() ,求
,求![]() 的大小;
的大小;
(3)通过对以上的解题回顾,你发现![]() 与
与![]() 、
、![]() 三个角之间有怎样的大小关系?请把你的发现结论直接写出来.
三个角之间有怎样的大小关系?请把你的发现结论直接写出来.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的分式方程![]() ①和一元二次方程
①和一元二次方程![]() ②中,m为常数,方程①的根为非负数.
②中,m为常数,方程①的根为非负数.
(1)求m的取值范围;
(2)若方程②有两个整数根x1、x2,且m为整数,求方程②的整数根.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点![]() 是菱形
是菱形![]() 边上的一个动点,点
边上的一个动点,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向匀速运动到
的方向匀速运动到![]() 停止,过点
停止,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,已知
,已知![]() ,设点
,设点![]() 走过的路程为
走过的路程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() (当点
(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )
)

小腾根据学习函数的经验,对函数随自变量的变化规律进行了探究,下面是小腾的探究过程,请补充完整;
(1)按照下表中自变量的值进行取点,画图,测量,分别得到了以下几组对应值;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数的图像;
,并画出函数的图像;

(3)结合函数图像,解决问题,当点![]() 到直线
到直线![]() 的距离恰为点
的距离恰为点![]() 走过的路程的一半时,点P走过的路程约是
走过的路程的一半时,点P走过的路程约是 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD![]() DF,连接CF、BE.
DF,连接CF、BE.
(1)求证:DB![]() DE;
DE;
(2)求证:直线CF为⊙O的切线;
(3)若CF![]() 4,求图中阴影部分的面积.
4,求图中阴影部分的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB.CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
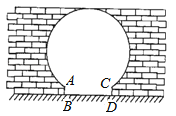
A.2米 B.2.5米 C.2.4米 D.2.1米
查看答案和解析>>
科目: 来源: 题型:
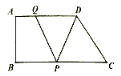
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 以每秒2个单位长的速度运动,动点
以每秒2个单位长的速度运动,动点![]() 同时从点
同时从点![]() 出发,在边
出发,在边![]() 上以每秒1个单位长的速度向点
上以每秒1个单位长的速度向点![]() 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为
运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为![]() (秒),
(秒),
(1)①设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 为何值时,
为何值时,![]() ?
?![]() 能不能等于
能不能等于![]() ?为什么?
?为什么?
(2)①当![]() 为何值时,
为何值时,![]() ?
?
②当![]() 为何值时,点
为何值时,点![]() 是在
是在![]() 的垂直平分线上?
的垂直平分线上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com